[CS231] Lec2. Image Classification with Linear Classifiers

⭐Key Points

• Image Classification에서 주로 대두되는 어려움들
• k-Nearest Neighbor Classifier
• Linear Classifier - SVM vs Softmax

1. Image Classification

• Image Classification은 입력 이미지가 어떤 카테고리에 속하는지 고르는 것을 말한다.

  01. Tasks of Image Classification

  • Semantic Gap
    • 인간과 다르게, 컴퓨터에게 고양이 이미지는 단지 아주 큰 격자 모양의 숫자집합일 뿐이다.
    • 따라서 같은 대상이라도 아래의 변화들이 생기면 이미지를 분류하기가 어려워진다.
  • Viewpoint variation: 카메라의 방향에 따른 변화
  • Illuminiation: 조명에 따른 이미지 밝기 변화
  • Background Clutter: 배경과 유사한 색상의 대상
  • Occculusion: 객체 가려짐에 따른 변화
  • Deformation: 객체 변형에 따른 변화
  • Intraclass variation: 같은 카테고리 안에서 대상의 다양성

  • Context: 맥락에 따른 구분

  • 이미지를 구분하기 위해서 하드코딩으로 알고리즘을 작성하는 것은 불가능하다.
  • 따라서 Data-Driven Approach(데이터 중심 접근)가 필요하다.
  • 머신러닝 알고리즘을 통해 classifier를 훈련하고 새로운 이미지에 대해 classifier를 테스트한다.

2. Nearest Neighbor Classifier

01. Nearest Neighbor

• 간단한 Data-Drivne Approach로서의 image Classifier
• train data를 기억하고, test data를 기존의 train data와 distance metric을 통하여 비교하여 가장 유사한 레이블 유추한다.
• 하나의 test data에 대해 예측을 진행할 때, 모든 train data를 검토해야하기에 O(N)으로 예측을 진행하는 데에 너무 오랜 시간이 걸린다.

02. K-Nearest Neighbor

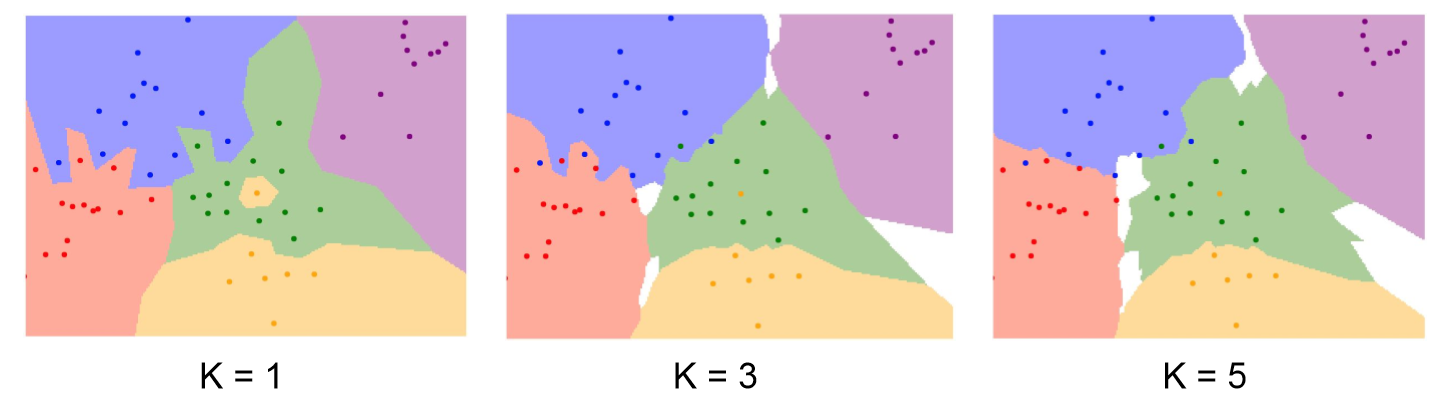
• 거리기반 분류 알고리즘으로 test data에 대해 거리가 가까운 k개의 다른 data의 label을 참고하여 분류하는 알고리즘
• Supervised Learning(지도학습)의 한 종류로 기존 관측치인 label 값이 존재하기에 비지도 학습인 Clustering과는 차이가 있다.

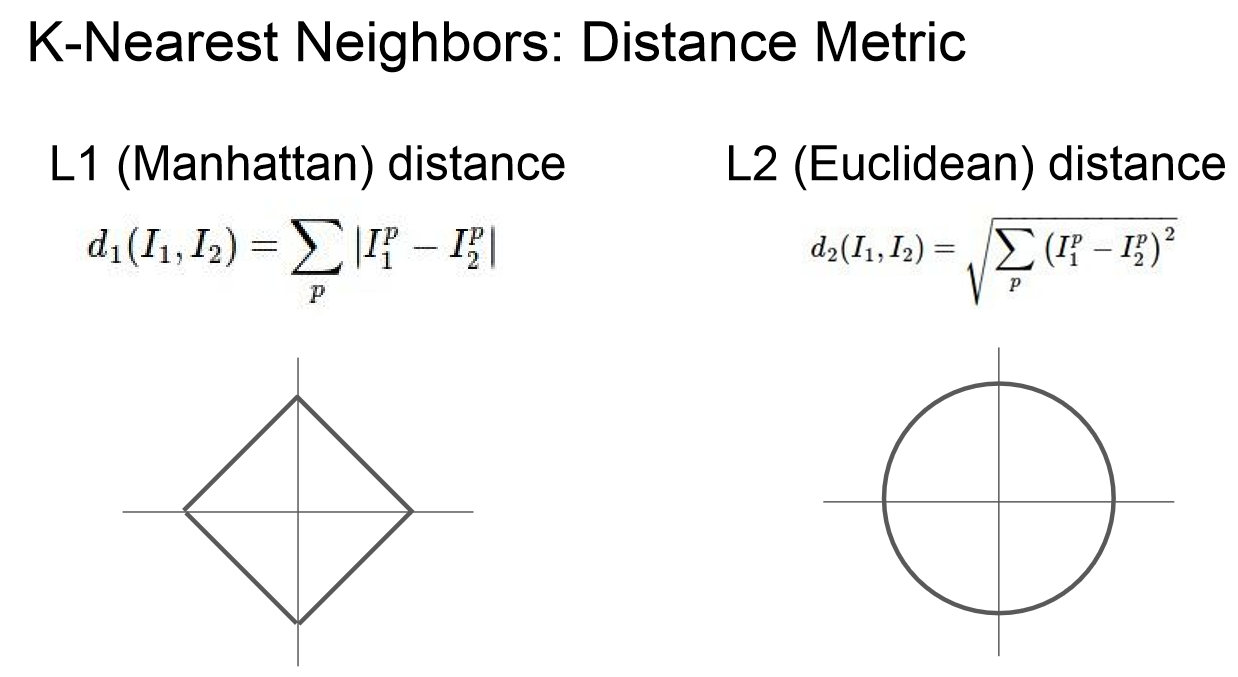
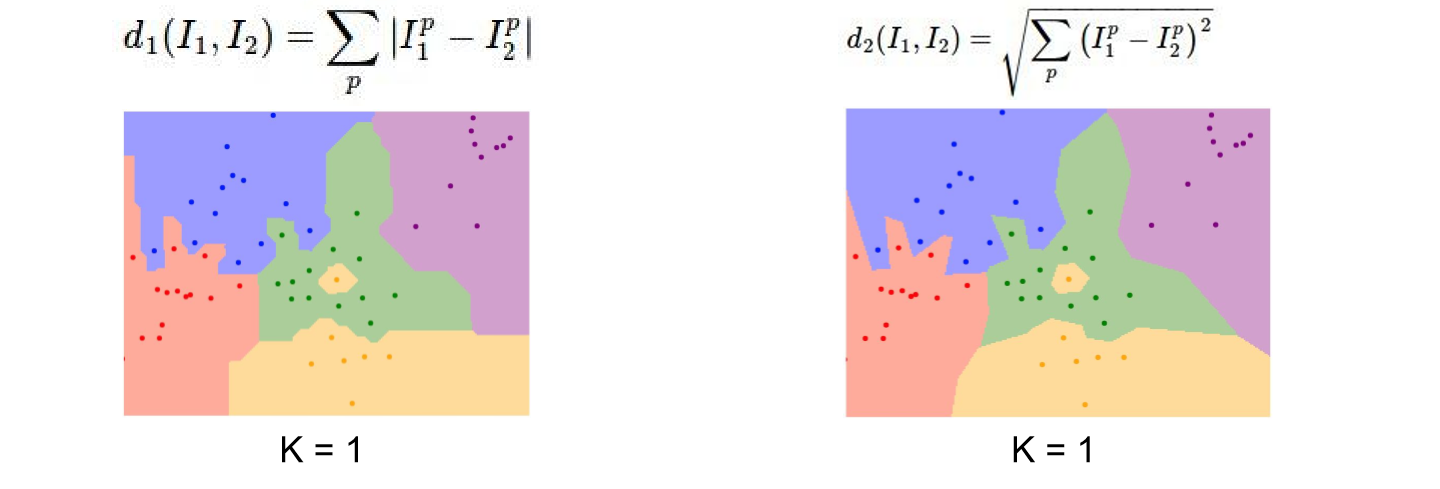
• Nerest Neaighbor 알고리즘을 사용할 때는 train data와 test data를 비교할 때 어떤 기준으로 거리(유사성)를 계산할 지 선택해야한다.
• L1 Distance: 절댓값을 이용하여 거리를 계산한다. 좌표계에 따라 영향을 많이 받기에 data들이 각각의 개별적 벡터(특징)을 가지고 있다면 유용하다.
• L2 Distance: 유클리디안 거리를 통해 계산한다. data들 간의 실질적 특징 차이를 잘 모를 경우 더 나을 수 있다.

03. Setting Hyperparameters

• 앞서 k-NN 알고리즘은 k값으로 어떤 값을 사용할 지, distance matrix로 어떤 것을 사용할 지 등을 선택해야했다.
• 이렇게 모델링을 할 때 사용자가 직접 세팅해주는 값을 hyperparameter라고 한다.
• Hyperparameter를 설정할 때, 대게 여러 경우들을 해보고 가장 좋은 성능을 낸 hyperparameter를 선택을 한다.
• 그 방법 중 2가지를 소개하고자 한다.

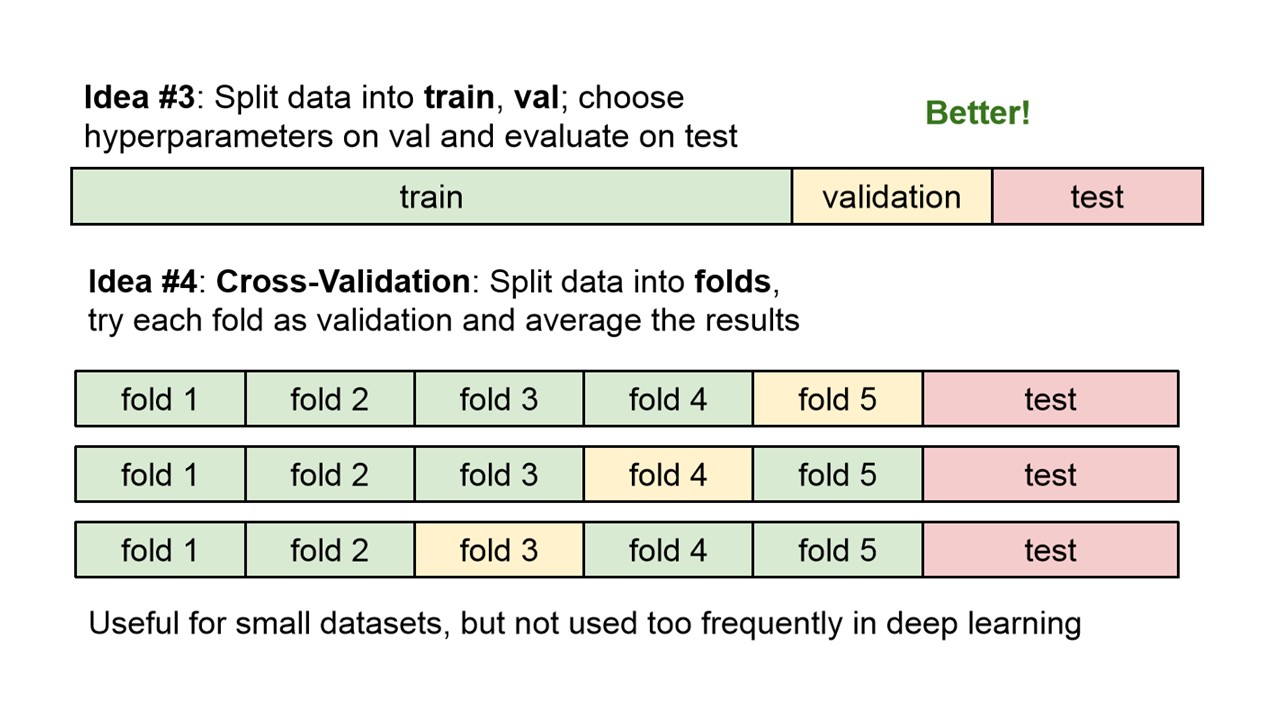
• Validation set 이용하기
  • test data는 test set에 overffiting되는 현상을 방지하기 위해 정말 마지막으로 모델 성능 측정을 하기 위해 1번만 사용하는 data이다
  • 따라서 validation set을 따로 두어 이를 통해 최적의 hyperparameter를 구하는 방법이다.
• Cross-Validation(교차검증)
  • data를 여러 fold로 쪼개고, validation set을 바꿔가며 성능을 측정한 결과의 평균을 모델의 성능으로 이용하는 방법이다.
  • 이를 통해 특정 validation set에 overfitting 되는 현상을 방지할 수 있고, 모든 데이터셋을 훈련에 사용할 수 있다는 장점이 있다.
  • Iteration 횟수가 너무 많아 시간이 오래걸려 dataset이 작을 때 주로 사용한다.

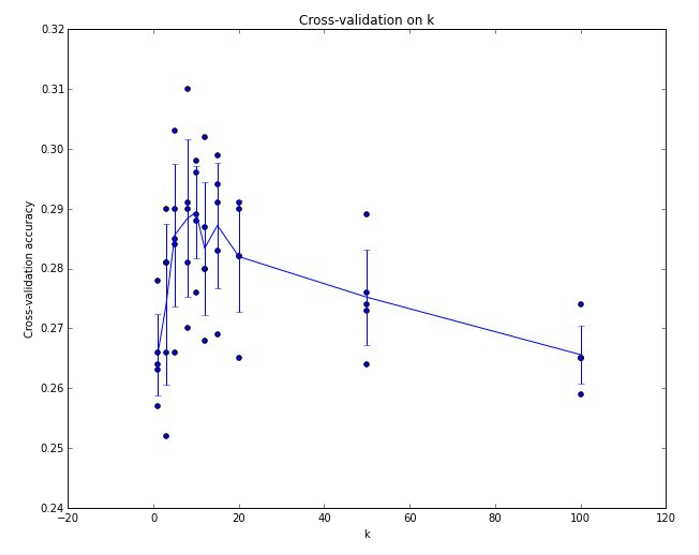
• 위 이미지는 5-fold cross validation 적용한 결과 그래프이다.
• 최적의 hyperparameter k는 대략 7로 나온 것을 확인할 수 있다.

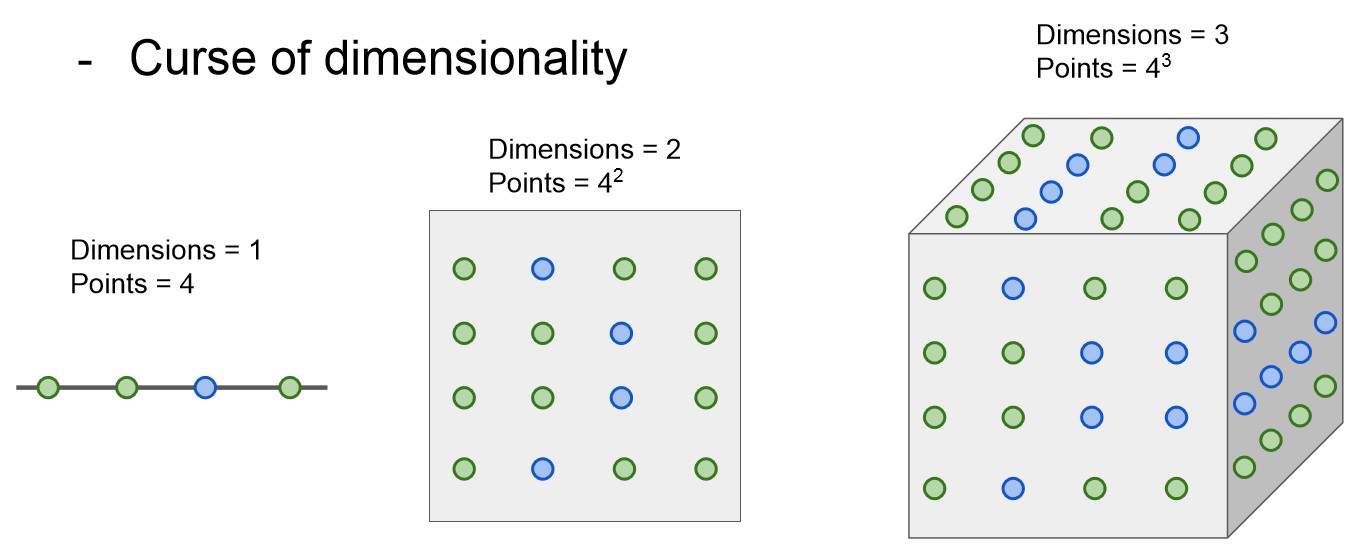
• 하지만 k-Nearest Neighbor 알고리즘은 이미지에서 픽셀 거리를 계산할 때는 사용하지 않는다.
• 차원이 늘어남에 따라 조밀하게 집단을 분류하기 위해 필요한 데이터 수가 기하 급수적으로 늘기 때문이다.

3. Linear Classifier

01. Linear Classifier

• 이미지 분류를 위해 parametric approch가 도입되었고, linear classifier가 그 가장 기본이 된다.
• Linear classier는 Neural Network의 가장 기본이 되는 블럭이기에 중요하다.
  
  
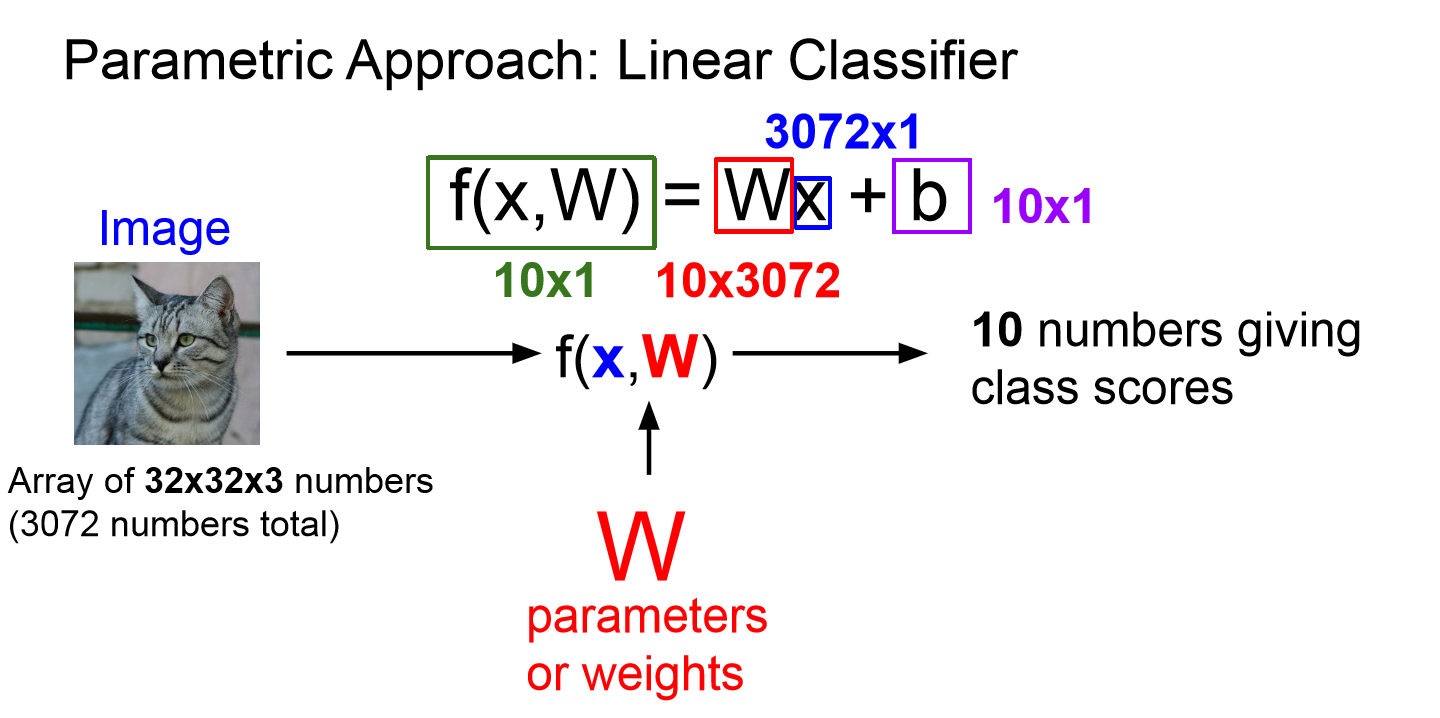
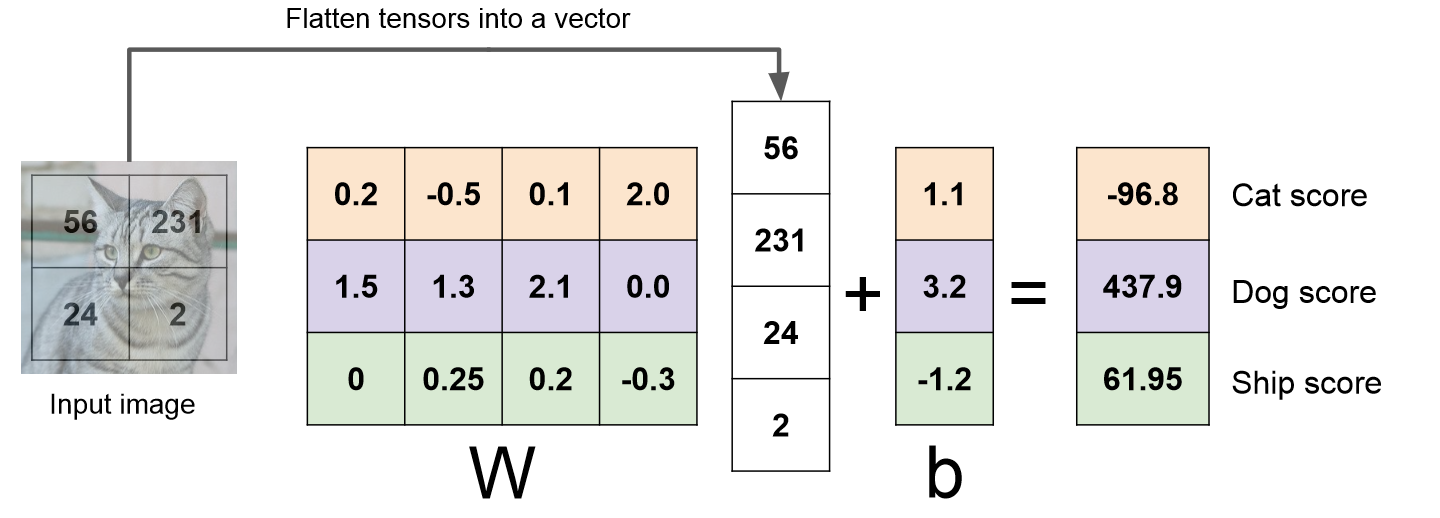
• train data의 정보를 요약하여 파라미터 W(가중치)에 모아준다.
• 더이상 test할 때 모든 train data가 필요하지 않고 W만 있으면 되기에 빠르고 효율적으로 예측을 진행할 수 있다.

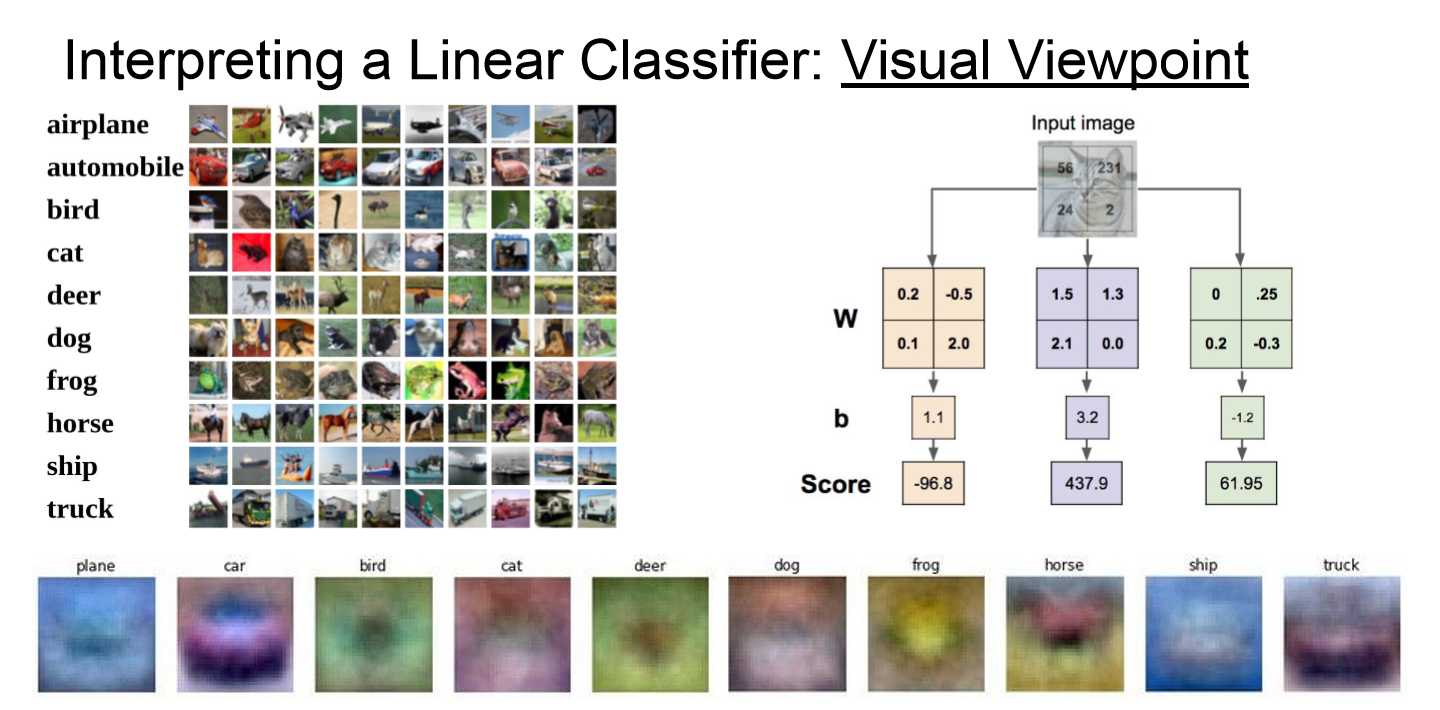
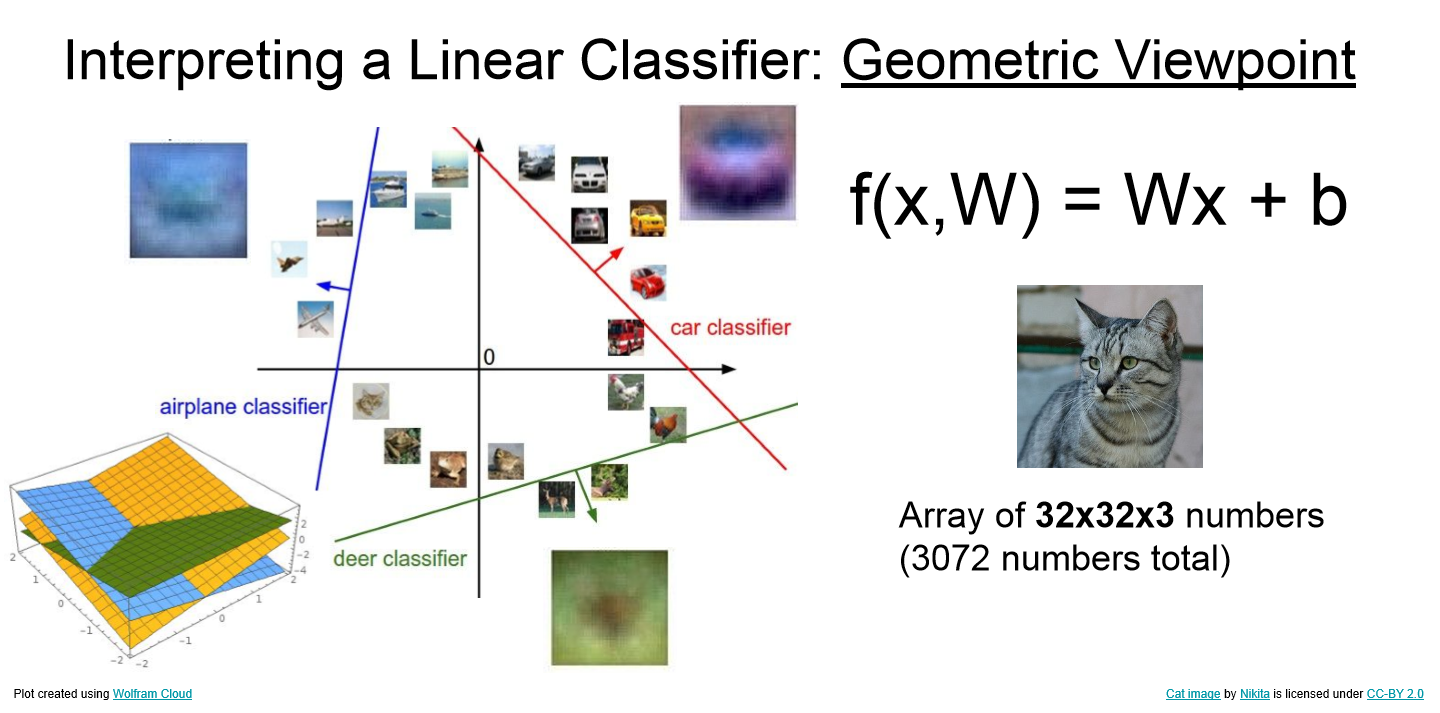
• 위 이미지를 통해 linear classifier가 image를 분류하는 방법을 보다 직관적으로 받아들일 수 있다.

• 그렇다면 좋은 W를 어떻게 얻느냐에 대한 의문이 생기는데, 이때 필요한 것이 loss function(손실함수)이다.
• Loss function은 모델의 예측값과 실제값의 차이를 표현하는 지표로 이 오차를 최소화하는 방향으로 모델의 파라미터 W를 학습시켜 최적의 모델을 찾게된다.
• 예시의 3가지 이미지를 보면 자동차는 정답 클래스의 스코어가 가장 높아 좋은 W를 가지고 있지만, 고양이의 경우 정답 클래스의 스코어가 가장 높지 않아 나쁜 W를 가지는 것을 확인할 수 있다.

02. SVM(Support Vector Machine)

• 대표적인 linar classifier의 loss function으로 SVM(Suppoer Vector Mashine)이 있다.
• 정답 label의 스코어와 정답이 아닌 label의 스코어의 차이가 셋팅한 margin(예시에서는 1)보다 크면 loss를 0으로 가진다.
• 특징으로 W가 작아 모든 s가 0에 가까우면 L_i는 C(클래스개수)-1이 된다. 이를 모델 학습 시 첫번째 iteration에서의 loss가 C-1인지 확인해봄으로서 디버깅툴로 이용할 수 있다.

03. Softmax

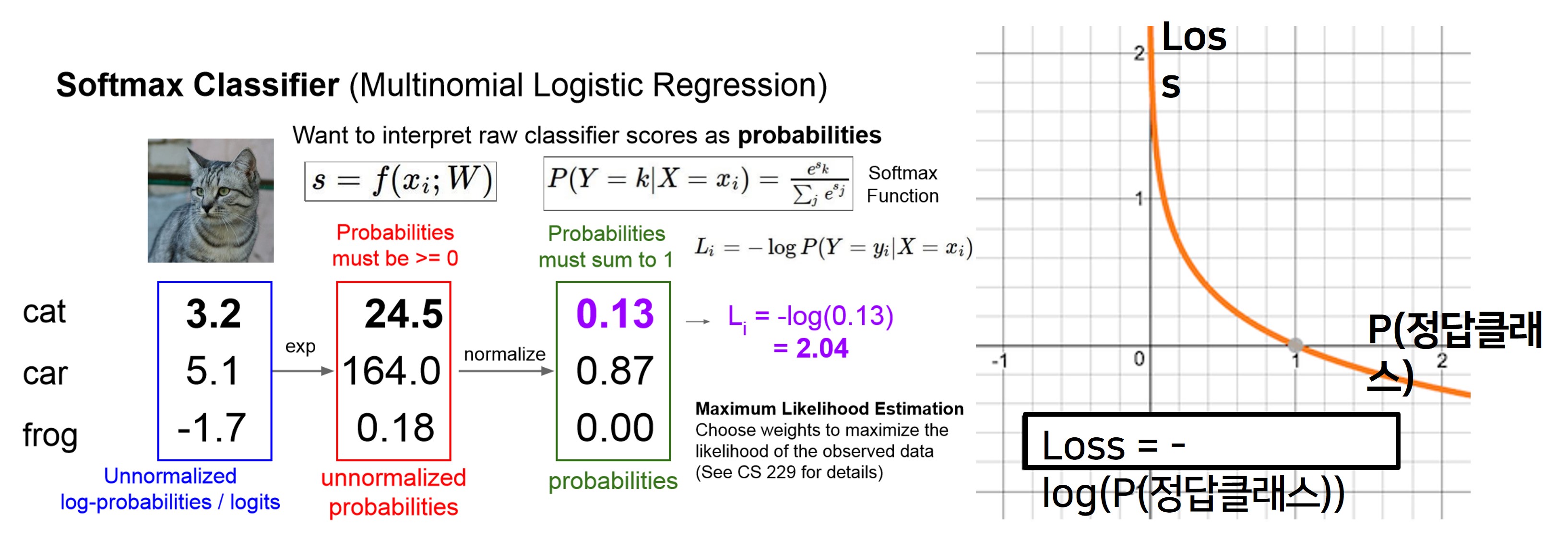
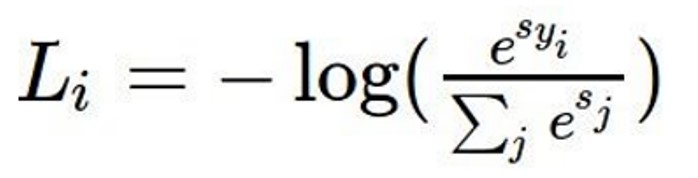
• 다음은 Softmax Classifier로 Softmax 함수를 통해 스코어를 지수화시켜 값을 모두 양수로 만들어주고, 이를 합이 1이 되도록 정규화 시켜줌으로서 확률 분포 를 계산한다.
• Softmax 함수 값은 0~1의 값을 가지게 되고, 모든 확률의 합은 1이 된다.
• x_i 데이터의 예측값이 y_i로 제대로 나올 확률을 “최대화“ 하고자 하기에, 이때 log를 취해 수학적으로 최댓값을 구하기 쉽게 해주고, 그것에 마이너스를 붙인 loss functio을 ＂최소화＂하는 것이 목표이다.
• 특징으로 s가 모두 0 근처에 모여있는 작은 수일 때 loss = -log(1/C)가 되기에, 이를 모델 학습 시 첫번째 iteration에서 디버깅툴로 이용할 수 있다.

04. SVM vs Softmax

• SVM은 loss를 최소화 하기위해 정답과 그 외 클래스 간의 스코어 차이에만 관심이 있기에, 차이가 일정 margin을 넘기면, 즉 loss가 0이 되면 성능개선에 신경 쓰지 않는다.
• 하지만 softmax의 경우 최대한 정답 클래스에 확률을 몰아넣기 위해서, 정답 클래스와 그외 클래스간의 차이가 클수록 loss가 줄어드는 것을 확인할 수 있다.

Summary

1. Image Classification

• 인간과 컴퓨터가 이미지를 보는 차이가 있어 컴퓨터가 이미지를 구분하기에 여러 어려움이 있다.
• 이를 Data-Drivien Approach로 머신러닝 알고리즘으로 classifier를 훈련하고 새로운 이미지에 대해 classifier를 테스트하여 이를 통해 이미지 분류가 가능하다.

2. Nearest Neighbor Classifier

• K-Nearest Neighbor는 test data에 대해 거리가 가까운 k개의 다른 data의 label을 참고하여 분류하는 알고리즘이다.
• 거리를 측정하는 방법으로 L1과 L2 Distance가 있는데,data들 간의 실질적 특징 차이를 잘 모를 경우 L2가 더 낫다.
• 다만, 차원의 저주로 인해 이미지 분류에서는 사용하지 않는다.
• 모델링을 할 때 사용자가 직접 세팅해주는 값을 hyperparameter라고 한다.
• Validation set을 이용하여 최적의 hyperparameter를 구한다.
• Test set은 모델의 마지막 성능 측정을 용도로 한 번만 사용한다.

3. Linear Classifier

• 파라미터 W(가중치)에 train data의 정보를 요약하여 빠른 예측이 가능하다.
• 모델의 예측값과 실제값의 차이를 표현하는 지표인 Loss function을 통해 모델의 성능을 정량화 할 수 있다.
• SVM(Support Vector Machine) loss는 정답 label의 스코어와 정답이 아닌 label의 스코어의 차이가 셋팅한 margin(예시에서는 1)보다 크면 loss를 0으로 가진다.
• Softmax loss는 Softmax 함수를 데이터 x에 대한 각 클래스의 확률 분포를 계산한다.
• SVM은 정답과 그 외 클래스 간의 스코어 차이에만 관심이 있지만, softmax는 최대한 정답 클래스에 확률을 몰아 넣는다.

개인 공부 기록용 블로그 입니다.