[CS231] Lec3. Regularization and Optimization

⭐Key Points
L1, L2 Regularization
Gradient Descent(경사 하강법)
Stochastic Gradient Descent(확률적 경사 하강법)
Adam Optimizer

1. Regularization

01. Regularization?

• 우리는 test set을 잘 분류해줄 일반적인 분류기를 찾는 것이기에, Loss가 0인 가중치 W를 채택하지 않는다.
• 따라서 Regularization이라는 규제항을 손실함수에 추가하여 모델을 단순화 함으로서 모델이 training set에서만 잘 예측하는 Overfitting(과적합) 현상을 방지한다.
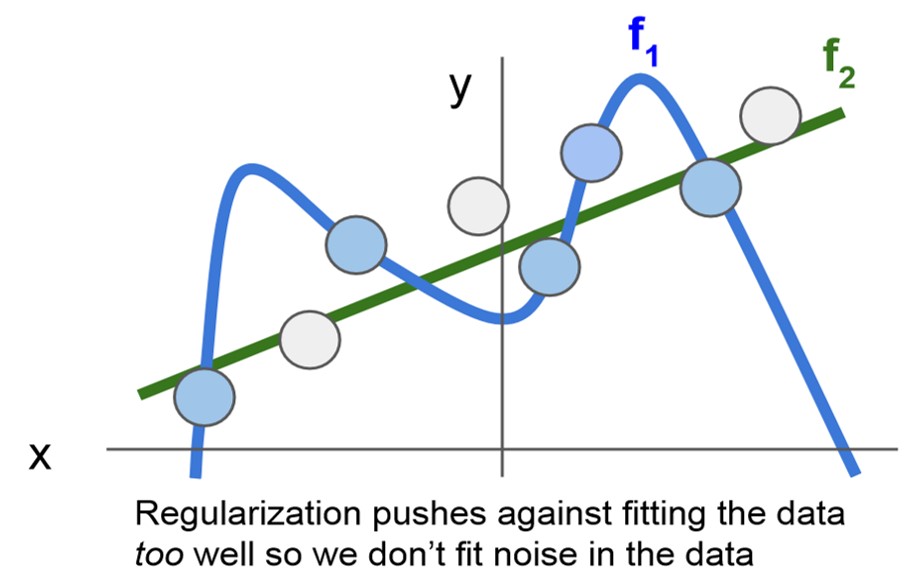
• 그래프를 통해 보다 직관적으로 확인할 수 있는데, 파란색 그래프 f1과 초록색 그래프 f2를 비교해보면 F1의 경우에 training set인 파란 포인트는 f2에 비해 정확히 예측하지만 test set에 해당하는 흰점에 대해서는 f2보다 안좋은 예측을 하는 것을 확인할 수 있다.
• 따라서 우리는 f1에 규제항 f2를 추가하여 보다 일반적인 모델을 얻고자한다.

02. Regularization Techniques

• 다음으로 여러 Regularization 기법들에 대해 알아본다.
• Regularization은 그 방법에 따라 정의하는 복잡도가 다르기에 적합한 regularization 기법을 적용하는 것이 필요하다.

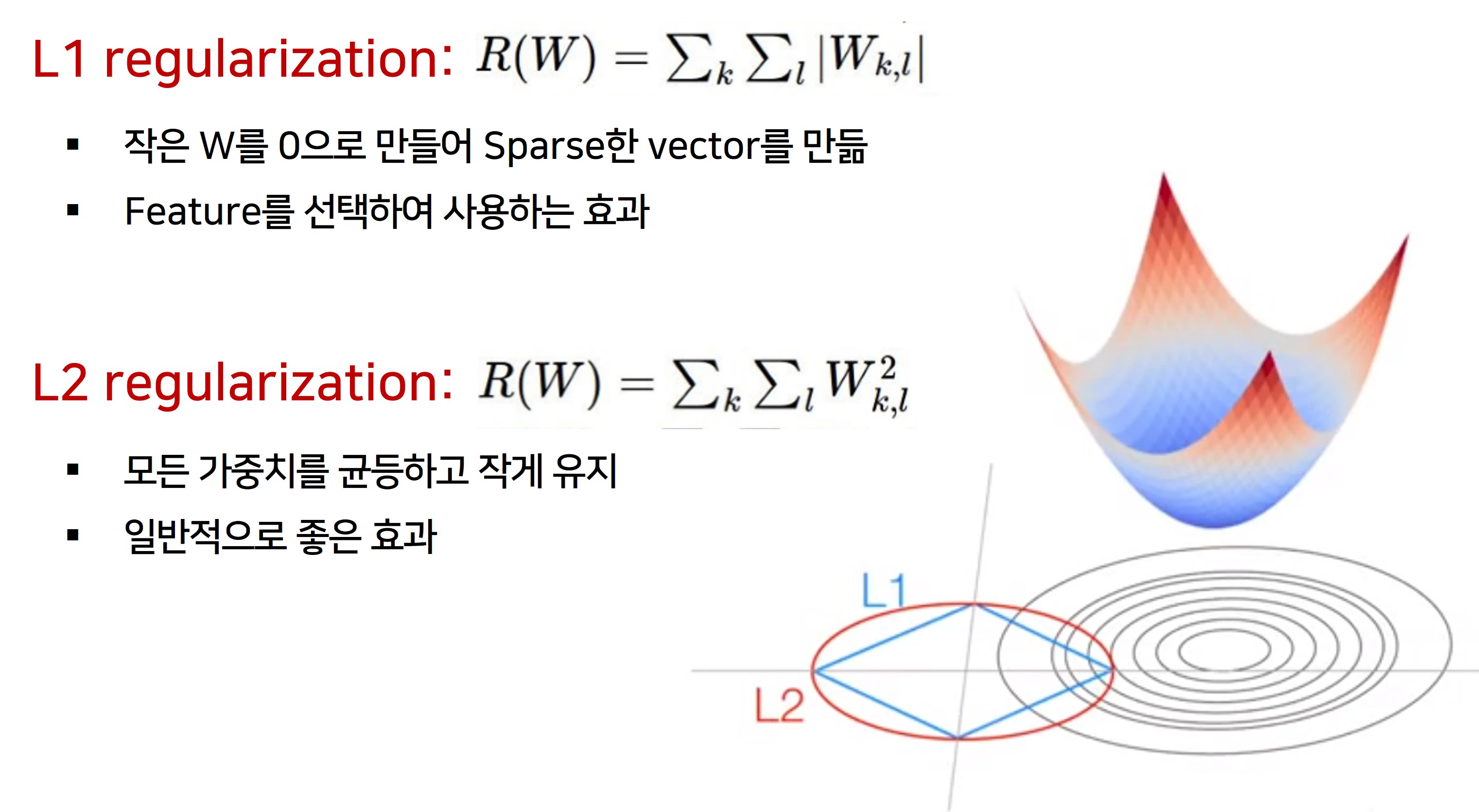
• L1을 적용하면 작은 W가 0이 되는 경향이 있어 보다 Sparse한 weight를 만든다.

• 따라서 중요한 weight만 선택하게 되고 나머지 weight는 0이 되는 효과를 얻을 수 있어서 Feature를 선택하여 사용하는 효과를 준다.

• L2는 모든 가중치를 균등하고 작게 유지하려고 한다.
• Regularization 값을 Loss에 더하기에 학습에 방해가 되지 않도록 연산결과가 작은 것을 선호한다.

• 따라서 L2가 일반적으로 좋은 효과를 내게 된다.

• 그래프를 보면 보다 이해하기가 쉬운데요, L1과 L2의 범위 안에서 최솟값이 수렴하게 되는데, L1은 꼭지점을 향해 수렴하여 W가 0이 되고, L2의 경우 균등한 값을 향해 수렴하게 되는것을 확인할 수 있다.

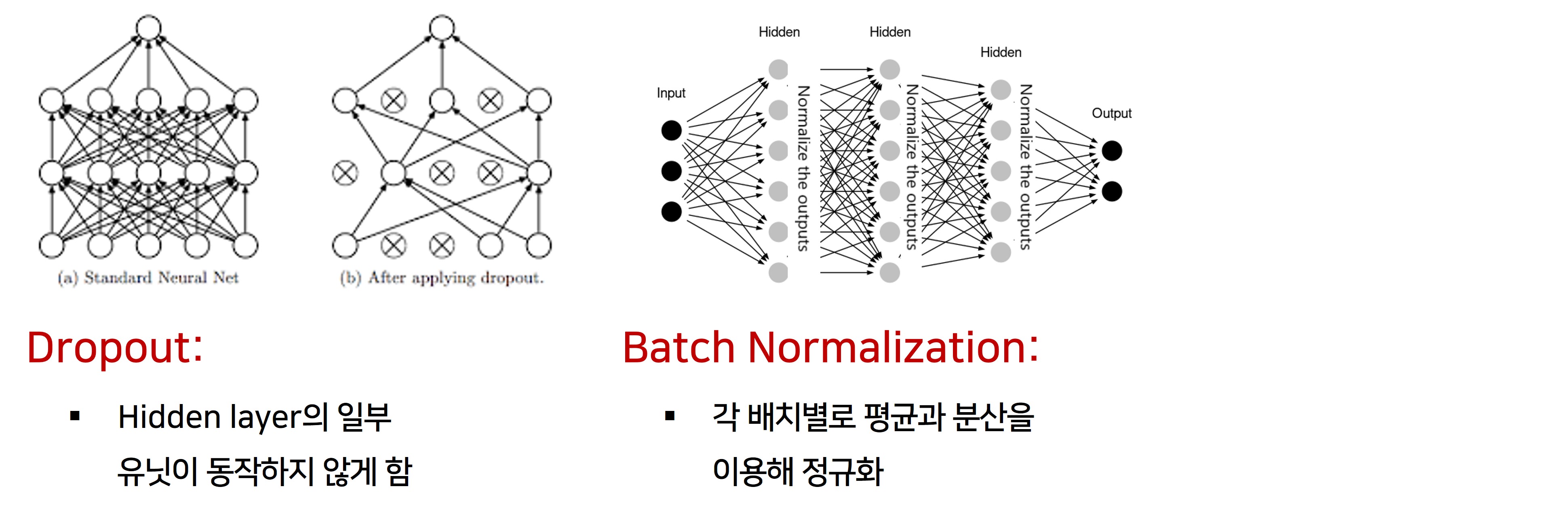
• 그 밖에 좀 더 복잡한 Regularization 방법들로
• Hidden layer의 일부 유닛이 동작하지 않게하는 DropOut
• 각 배치별로 평균과 분산을 이용해 정규화 하는 Batch Normalization
• 그리고 Stochastic depth, fractional pooling 등이 있다.
• 신경망에 적용되는 기법들이라 이정도로만 짚고 넘어간다.

2. Optimization

01. Optimization?

• 신경망에서는 loss function과 regularization 같은 것들이 매우 복잡해져, 명시적인 최적의 가중치를 한번에 구하는 것은 불가능하다.
• 임의의 지점에서 경사를 따라 내려가는 것 처럼 점진적으로 성능을 향상켜 최적의 W를 구한다.

02. Gradient

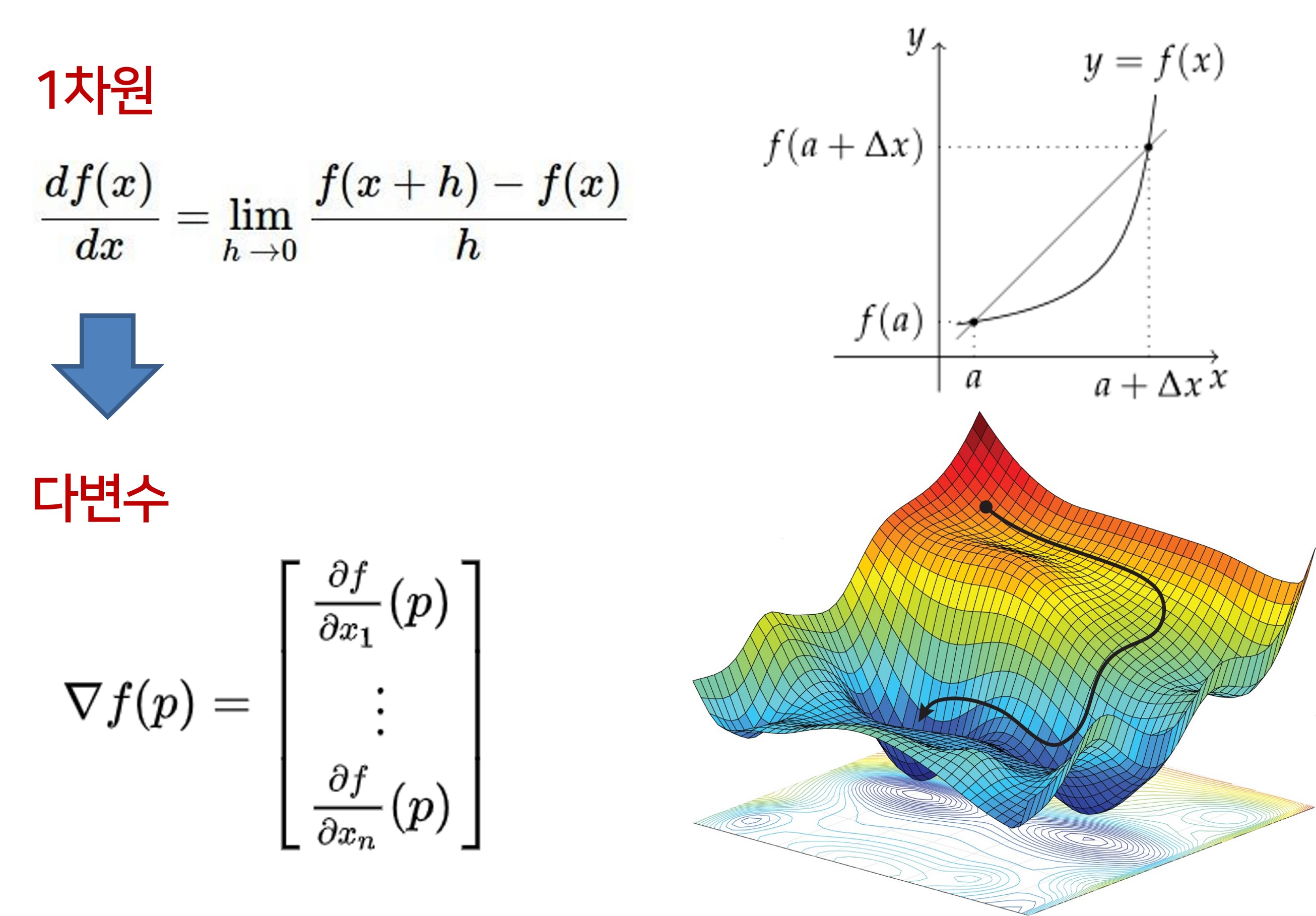
• 경사에 있어서 1차원에서는 도함수를 통해 한 점에서의 경사를 구한다.
• 하지만 실제로는 x가 벡터이기에 다변수 상황에서의 미분으로 확장하면, 경사는 벡터 x의 각 요소의 편도함수 집합으로 된 gradient가 된다.
• 또한 오른쪽 도함수의 그래프를 보면 알 수 있듯이 기본적으로 gradient는 올라는 방향이다.
• 하지만 우리는 오른쪽 아래 그림처럼 내려가는 방향이 필요하기에 negative gradien를 사용한다.

03. Numerical & Analytic Optimization

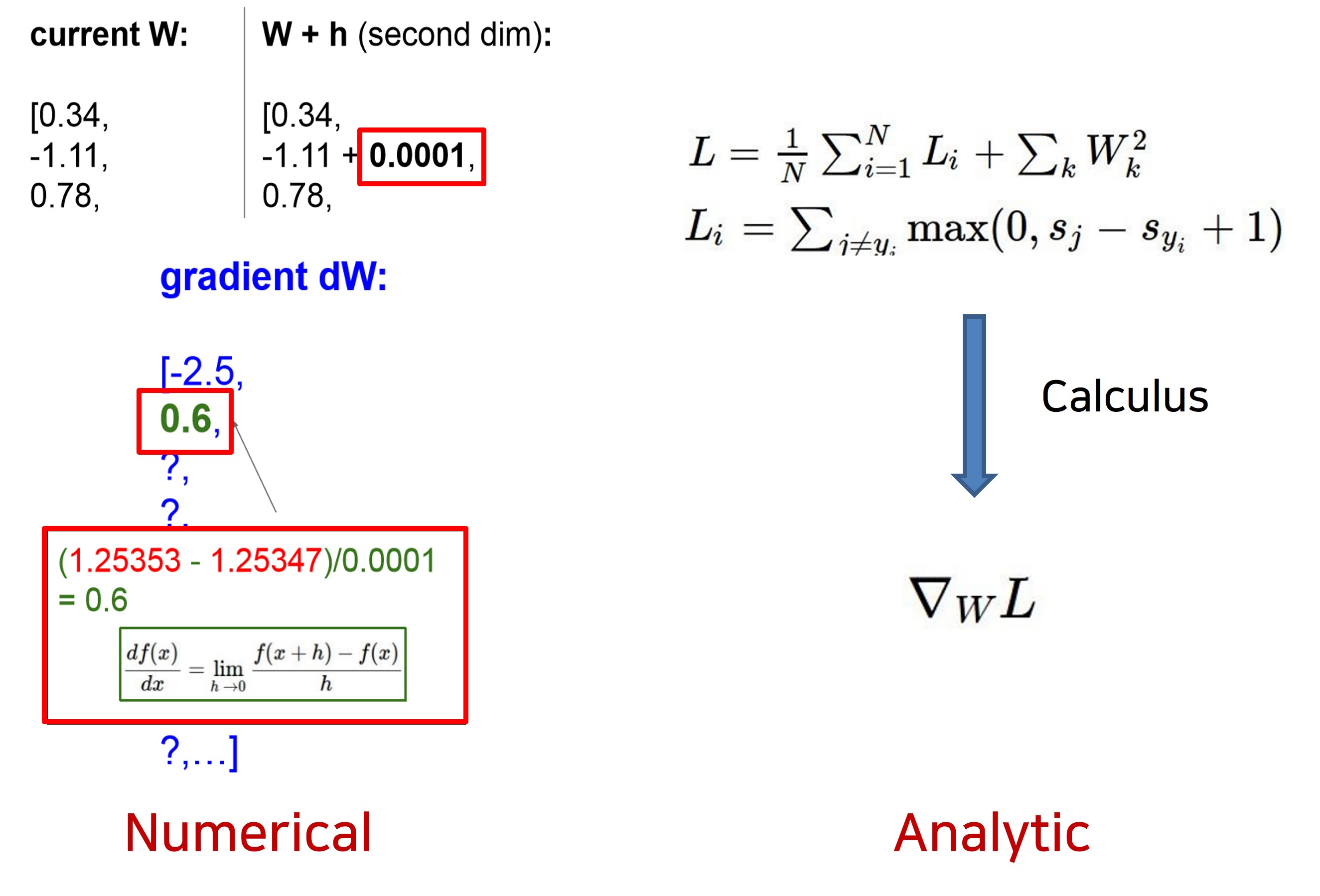
• 왼쪽 처럼 아주 작은 h를 이용해 하나하나 계산해 gradient를 구할 수 있다.
• 그런데, 이 방법은 시간이 너무 오래걸리기에 Loss function의 gradient를 미분을 통해 훨씬 정확하고 빠르게 계산한다.
• 그래도 Numerical한 방법이 수치 하나하나 확인이 가능하기에 디버깅툴로서는 유용하게 사용할 수 있다.

04. Optimization Techniques

• 다음은 Optimization 기법들에 대해 소개한다.

• Gradient Descent
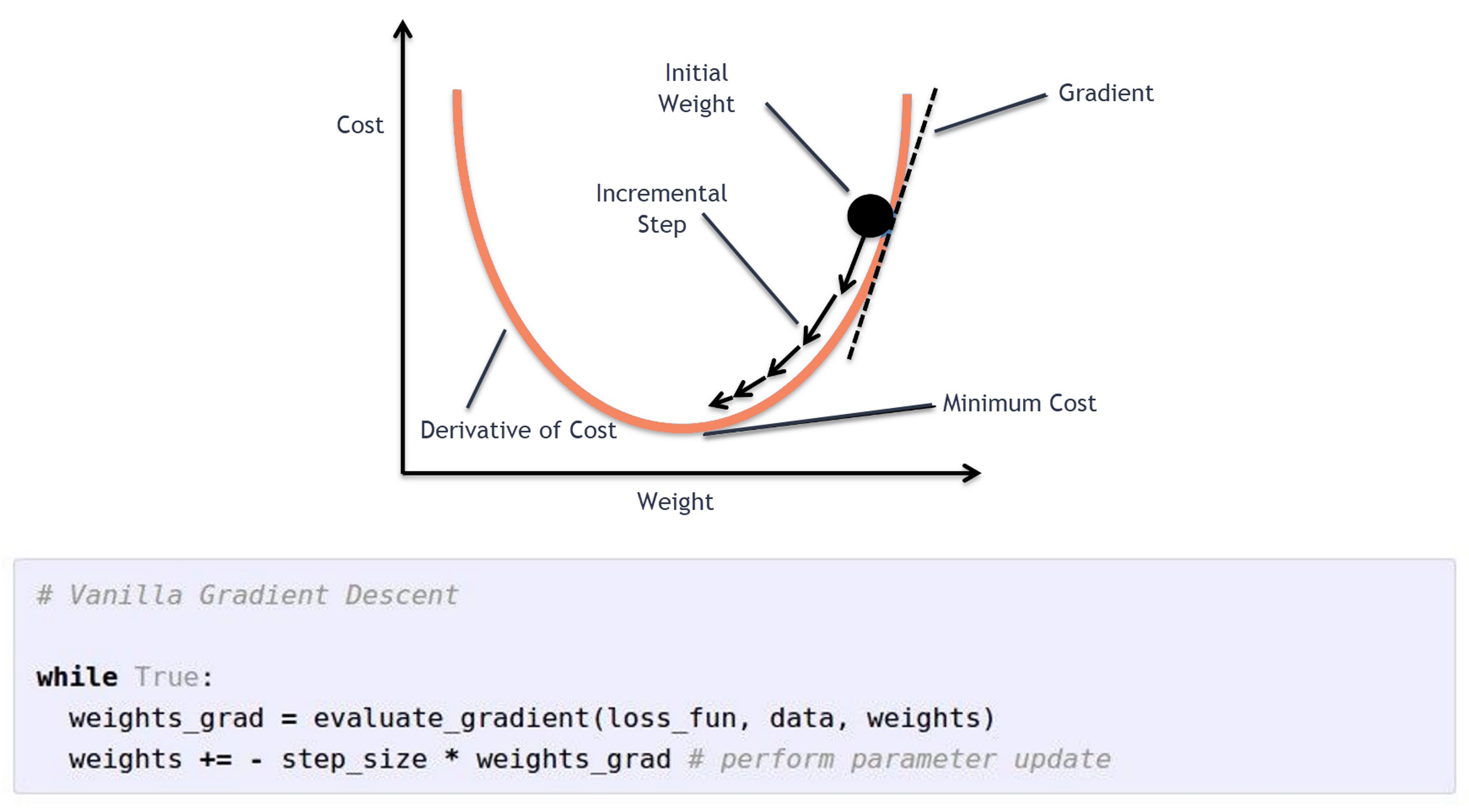
  • 먼저 경사하강법이라 불리는 Gradient Descent는 임의의 초기값을시작점을 잡고, Loss가 최소가 될때까지 W갱신을 반복하여 최솟값에 도달했을 때 해당하는 W를 찾아냅니다.
  • 이를 코드를 통해 나타내자면, 손실함수에 대한 gradien를 구해 최적치를 향한 방향을 구하고,
  • 이를 Step size 라고도 불리는 하이퍼 파라미터 Learning rate와 곱해주는 것을 확인할 수 있습니다.
  • 그리고 이를 이전의 가중치 W에 빼줌으로서 학습을 진행하는 것을 확인할 수 있습니다.
  • 전체 데이터셋(Batch) 단위로 학습을 진행하기에 계산횟수가 적고,
  • 전체 데이터셋에 대해 미분값을 계산하므로 안정적으로 수렴해나갑니다.
  • 하지만 학습 시간이 오래걸리고 상대적을 많은 메모리가 요구된다는 단점이 있습니다.
• SGD(Stochastic Gradient Descent, 확률적 경사하강법)
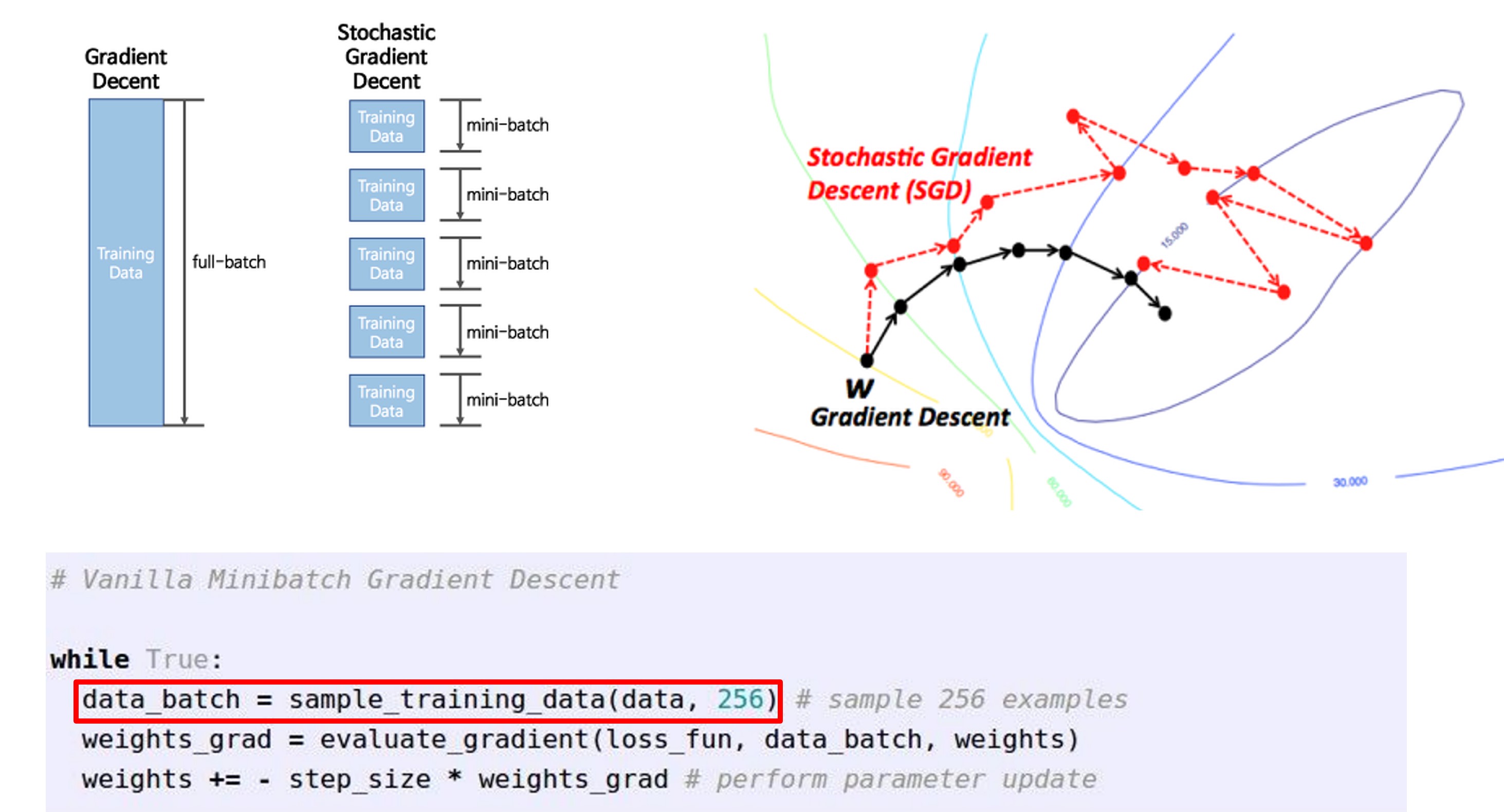
  • 전체 데이터셋(Batch)을 돌면서 gradient를 구하기엔 시간이 너무 오래걸리기에 2의 승수인 32/64/128 단위로 전체 데이터셋을 나눈 일부 데이터셋인 Minibatch를 통해, 반복적으로 전체에 대한 loss 추정치와 gradient의 추정치를 이용해 W를 갱신하는 것을 확률적 경사하강법, Stochastic Gradient Descent라고 합니다.
  • 예제코드를 보면 전제 데이터를 256으로 샘플링 한 것을 확인할 수 있습니다.
  • 상대적으로 헤매면서 나아가지만, 보다 빠르게 minimu에 도달가능합니다.
  • 또한 병렬 처리가 가능하기에 GPU를 이용하여 빠르게 계산 가능합니다.

  

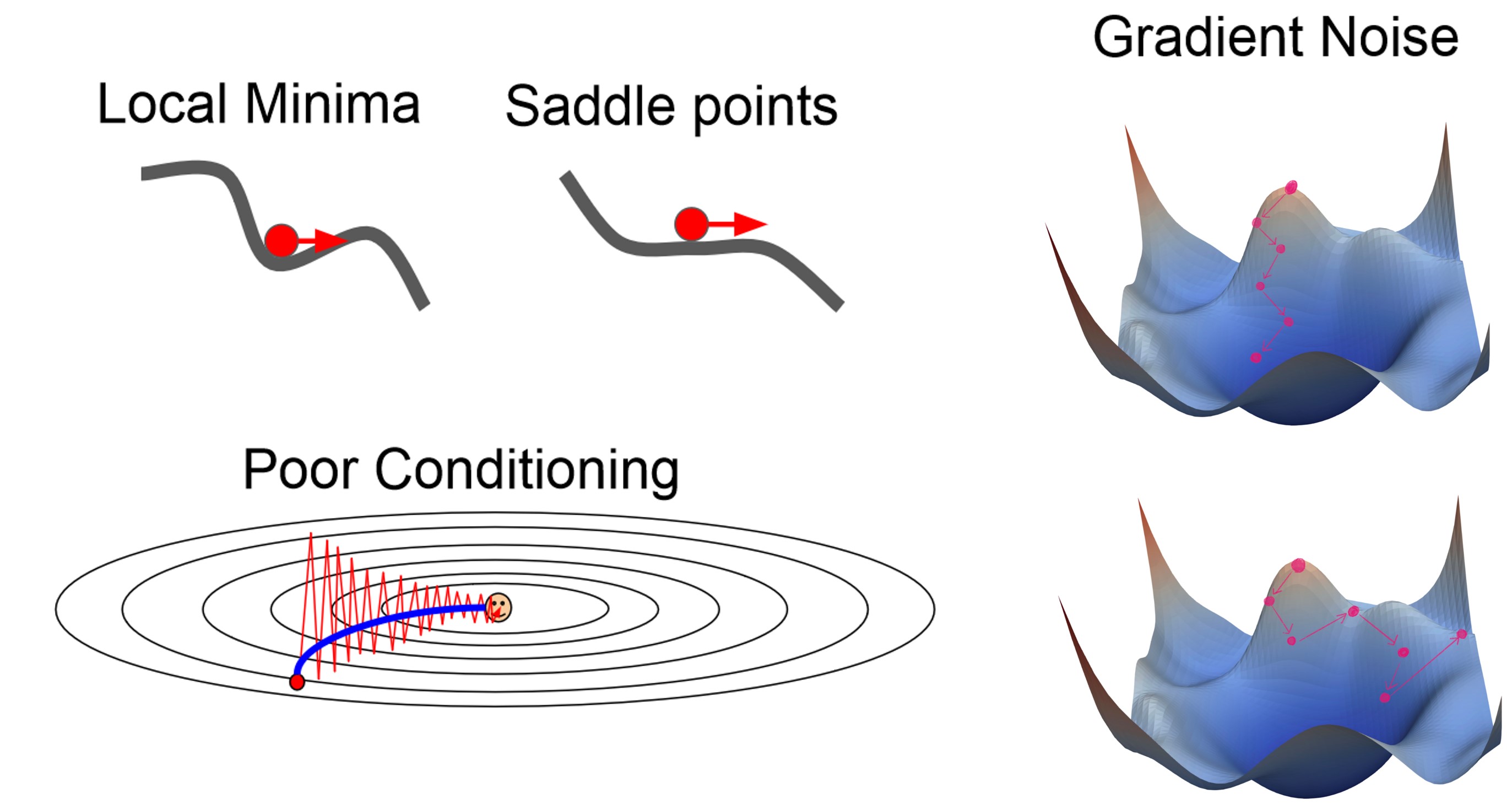
  • 하지만 SGD는 여러 단점이있는데요,
  • 모든방향에서 loss가 증가하여 빠져나오지 못하게 되는 Local minima나
  • Gradient의 값이 너무 작아 학습이 더디게 진행되는 Saddle points에 빠지면 최적값에 수렴하는데에 문제가 생긴다.
  • Local minima 고차원에서 매우 드물게 일어나지만, Saddle points 흔하게 발생하기에 문제가 된다.
  • 미니 배치단위로 gradient를 추정하며 학습하기에 방향을 헤매이며 최적값으로 나아가는 Poor Conditioning
  • Minibatch를 이용하기에 전체 데이터를 이용해 구한 gradient에 비해 오차가 존재할 수 있어, Global minima로 수렴해가는데에 어려움을 격는 Gradient Noise 문제가 발생할 수 있다.
• SGD + Momentum
  • SGD에 rho와 velocity를 통해 관성을 더해주는 방법입니다.
  • 이때 v항은 이전의 v를 이용하는데 여기에 이전의 gradient가 들어있기에
  • 이전 방향과 크기에 영향을 받아, Gradient의 방향이 바뀌더라도 이전 방향을 유지하여 일정하게 가속해 빠르게 나아갈 수 있습니다.
  • 예제 코드를 보면 기존에 dx만 더해곱해주던 SGD와 다르게 vx라는 항을 추가해준 것을 확인할 수 있습니다.
  • Saddle point에서 gradient가 0이 돼도 velocity가 유지돼 saddle point를 넘어갈 수 있습니다.
  • 보통 rho 값으로 0.9나 0.99를 사용합니다.

  

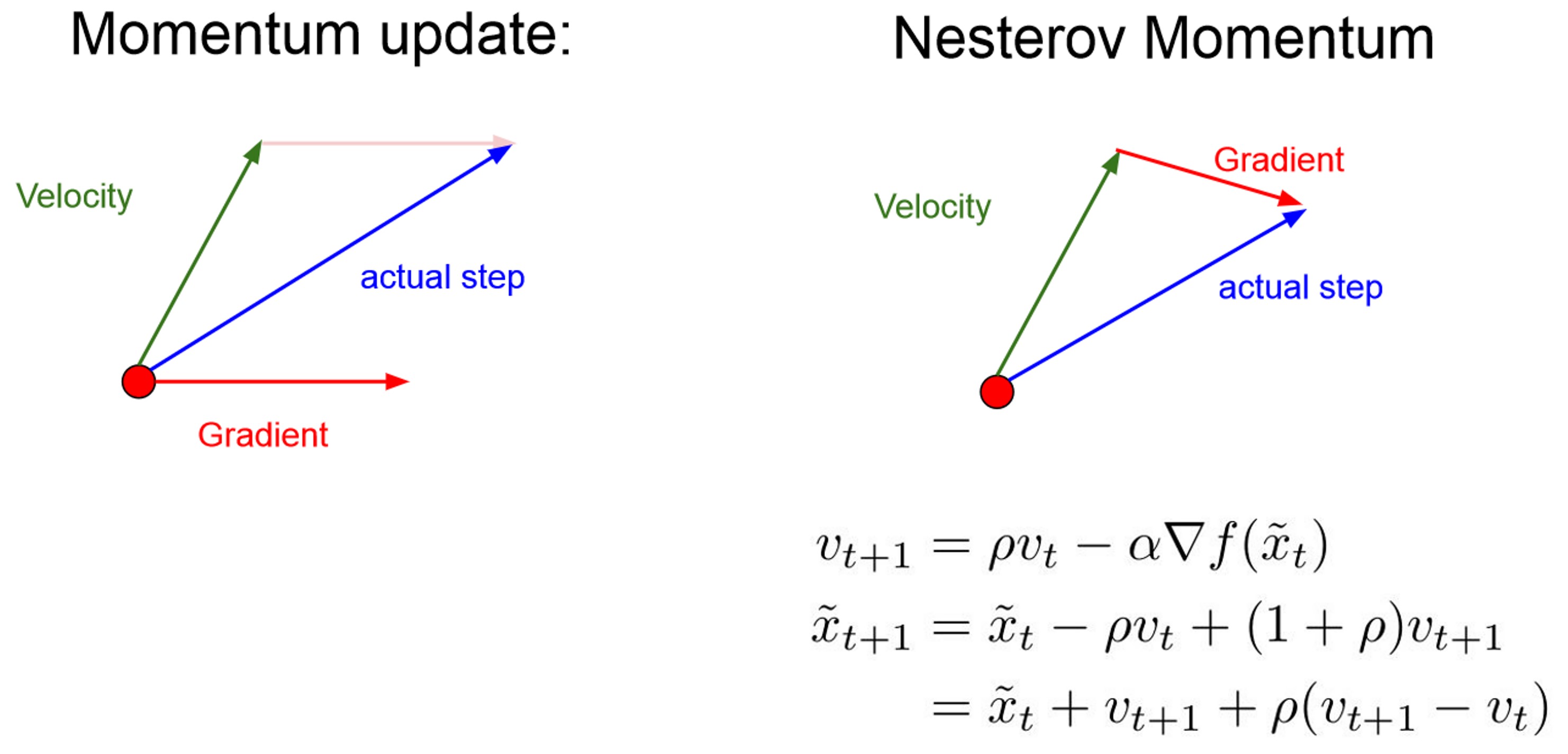
  • 그런데 velocity는 앞으로 나아갈 방향을 말하는 것이기에 미래에 대한 개념이 담겨있는데 이를 현재 상태의 gradient와 계산하여 실제 step을 계산해주는 것은 불합리적일 수 있습니다.
  • 따라서 verlocity를 통한 미래의 위치에서 gradient를 계산해 보다 합리적으로 step을 나아가는 방법이 Nestorv Momentum입니다.
  • 주로 Convex function 볼록함수에서 유용하다고 합니다.
• AdaGrad / RMSProp
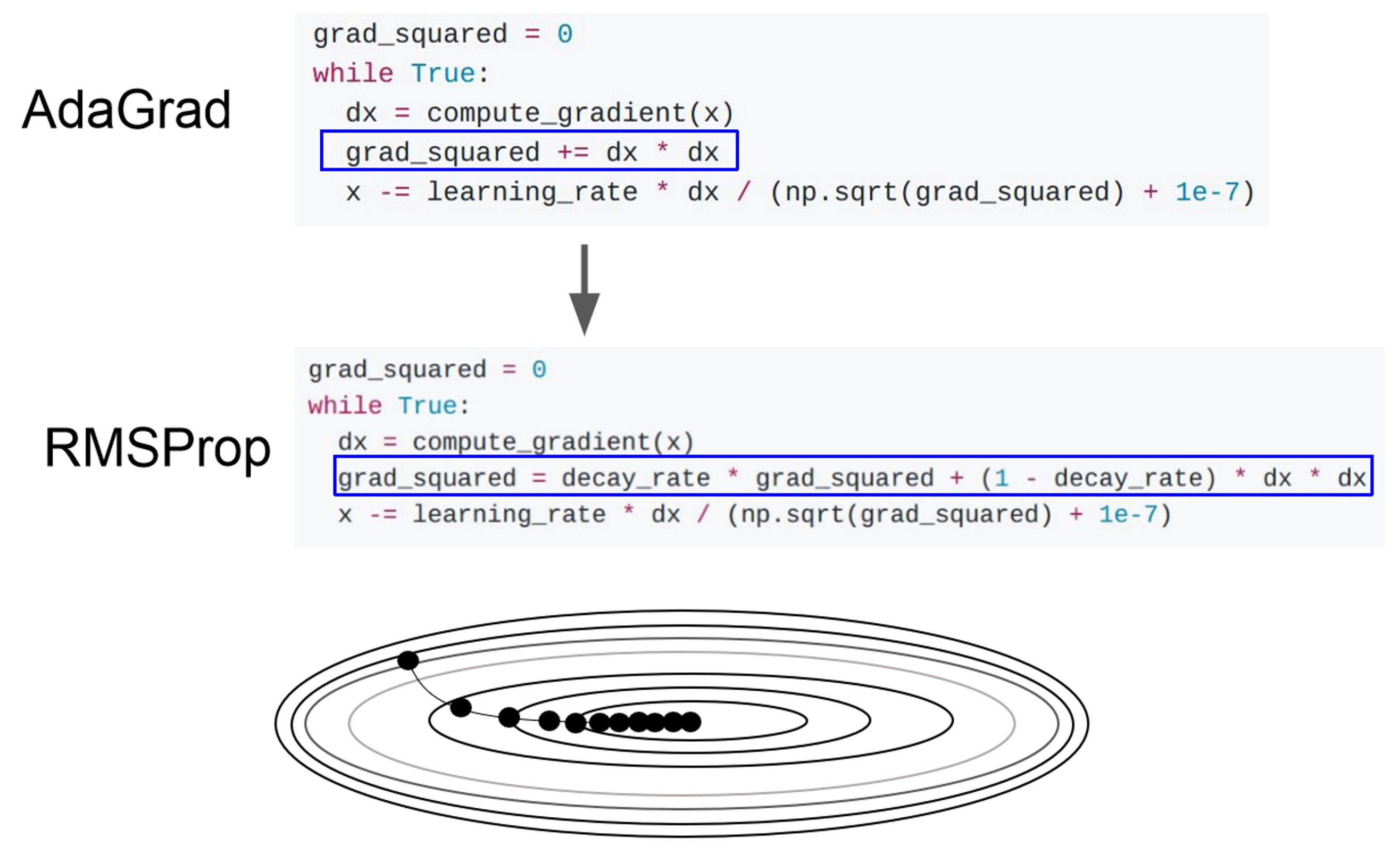
  • AdaGrad에서 step size가 너무 작아져 결국 갱신이 되지 않게 되는 문제를 해결하고자
  • Decay rate를 통해 과거의 gradient는 적게 최신의 gradient를 크게 반영하고, squared gradient가 무한히 커지는 것을 방지합니다.
  • 보통 decay rate로 0.9~0.999의 값을 씁니다.
• Adam
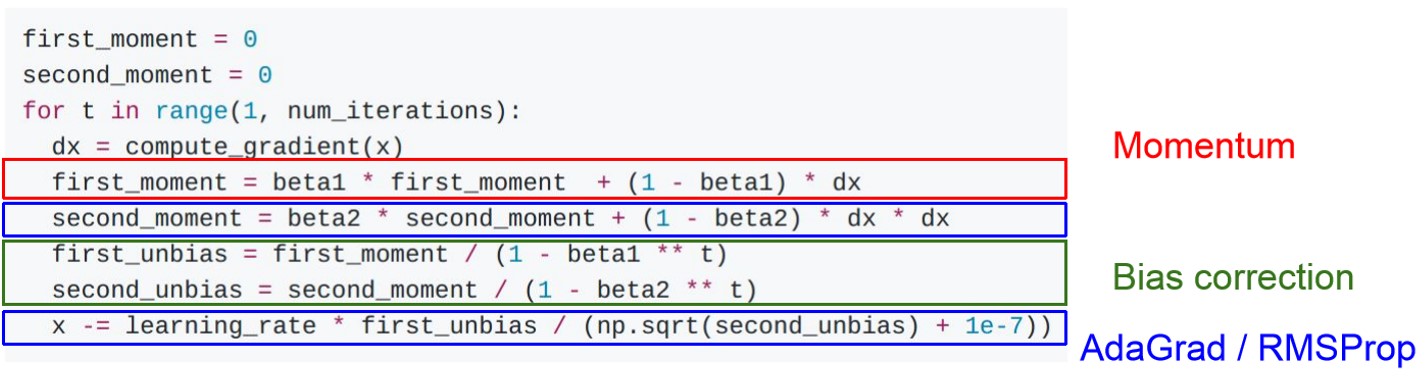
  • Momentum의 관성과 RMSProp의 squared gradient를 모두 반영한 Optimization입니다.
  • Momentum이 first momet로, RMSProp가 Second Momentum으로 적용 돼 있습니다.
  • Bias correction을 통해 첫 iteration에서 first와 second momen가 0으로 편향되는 것을 방지해줍니다.
  • Momentum의 rho에 해당하는 Beta1는 0.9, RMSProp의 decay rate에 해당하는 beta2는 0.999,
  • learning rate는 1e-3, 5e-4을 사용하는 것이 대게 좋은 출발지하고 합니다.
  • 왼쪽의 그래프를 보면 확실히 RMSProp와 Adam이 좋은 성능을 내는 것을 확인할 수 있는데요
  • 하지만 오른쪽 그래프를 보면 RMSProp는 local minimu에 빠진 반면 Adam은 Momentum을 통해 보완을 해주었기에 제대로 학습을 진행하는 것을 확인할 수 있습니다.
  • 실제로 딥러닝에서는 Adam Optimizer을 가장 많이 사용한다고 합니다.
• Learning Rate Decay
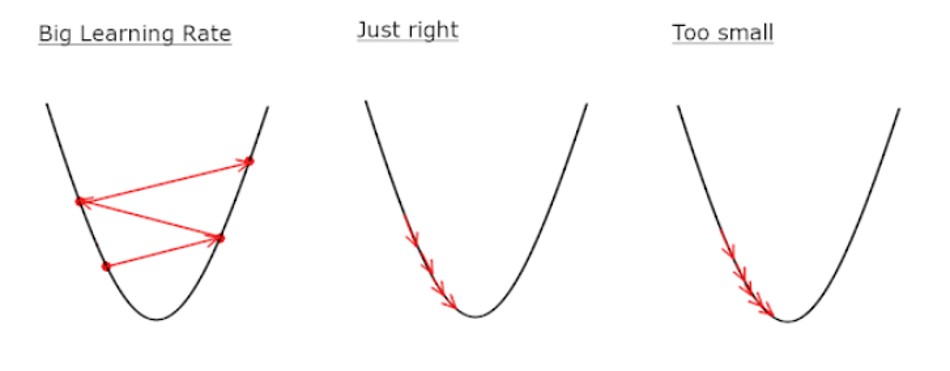
  • 앞선 gradient descent를 기반으로한 optimizer들에서 Step size, Learning rate라는 하이퍼 파라미터가 있었는데요,
  • Learning rate를 너무 크게 설정하면 학습이 jiggl거리고 너무 작게하면 학습이 오래 걸리고 제대로 안될 수 있기에 적절한 Learning rate를 설정해주는 것이 중요했습니다.
  • 이를 학습하는 동안 조절해준 Adagrad, RMSprop와 같은 optimizaer도 있었지만 추가적인 하이퍼 파라미터를 통해 조절해주는 방법도 있습니다.

  

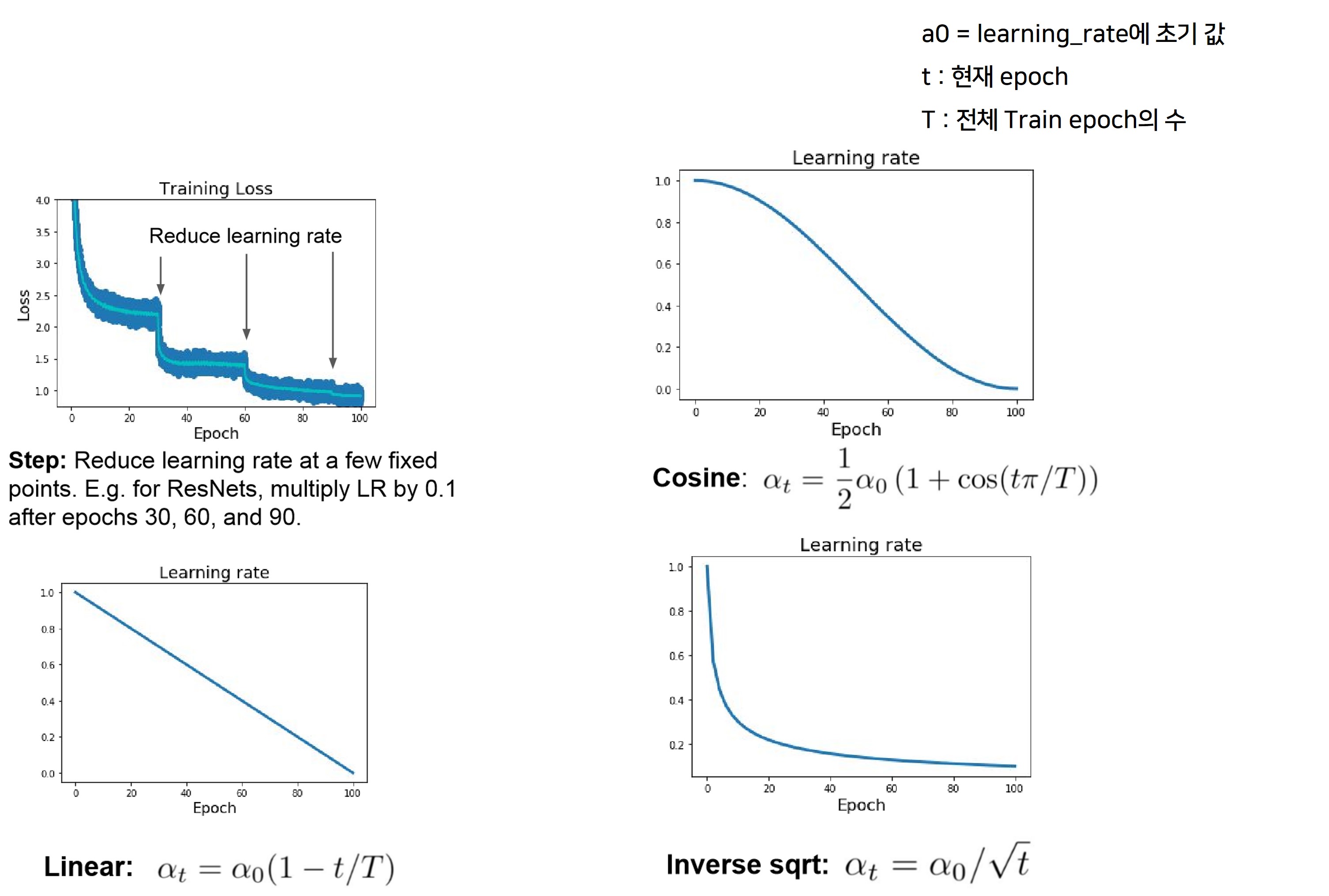
  • Learning Rate Decay인데요.
  • 처음 시작시 Learning Rate 값을 크게 준 후 일정 epoch 마다 값을 감소시켜서 적의 학습까지 더 빠르게 도달할 수 있게 하는 방법입니다.
  • 특정 epoch 구간(step) 마다 일정한 비율로 감소 시켜주는 방법을 Step Decay라 부릅니다.
  • Cosine Decay의 loss 그래프를 보면 위의 Step Decay와는 달리 안정적으로 끊김없이 loss가 감소하는 것을 볼 수 있습니다.
  • Cosine Decay에 비해 수학적으로 간단한 Lienar Decay 제곱근을 이용한 inverse square root decay가 있습니다.
  • 단 Learning Rate Decay는 처음부터 적용하는 하이퍼파라미터가 아니기에,
  • 우선 decay 없이 학습을 진행한 후 Loss Curve의 모양에 맞춰 적용을 해주는 것이 좋습니다.
  • 따라서 가장 좋은 것은 적절한 Learning Rate를 찾는것이라는 점을 말씀드립니다.
• Fisrt-Order Optimization
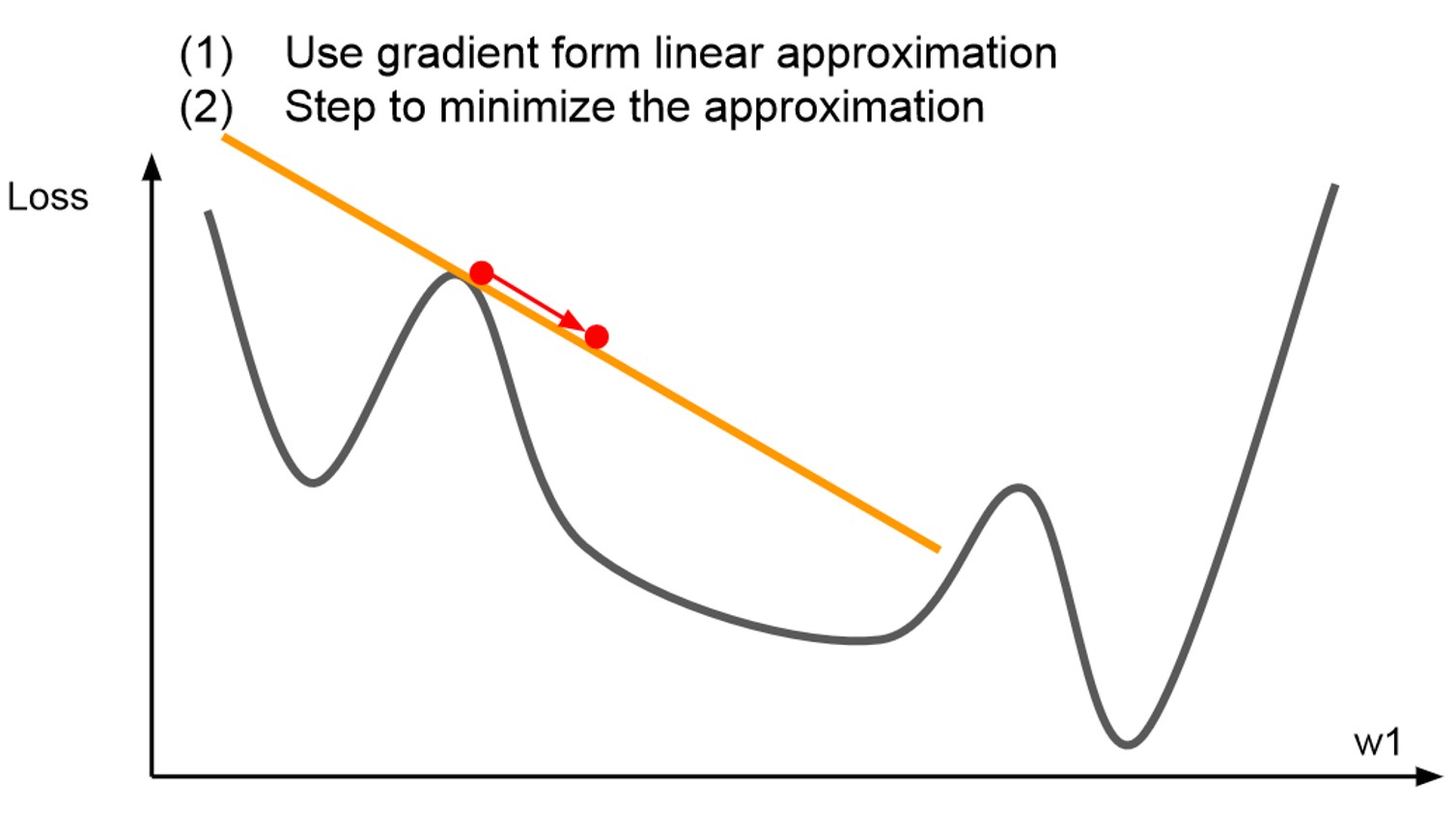
  • 지금까지 소개한 optimizer들은 우리가 잘 모르거나 복잡한 함수를 다루기 쉽고 이해하기 쉬운 다항함수로 대체하는 일종의 테일러 근사를 통한 1차 미분의 first-order 방법이었습니다.
  • 이는 gradient의 방향만을 알 수 있기에 많은 step을 나아갈 수 없었습니다.
• Second-Order Optimization
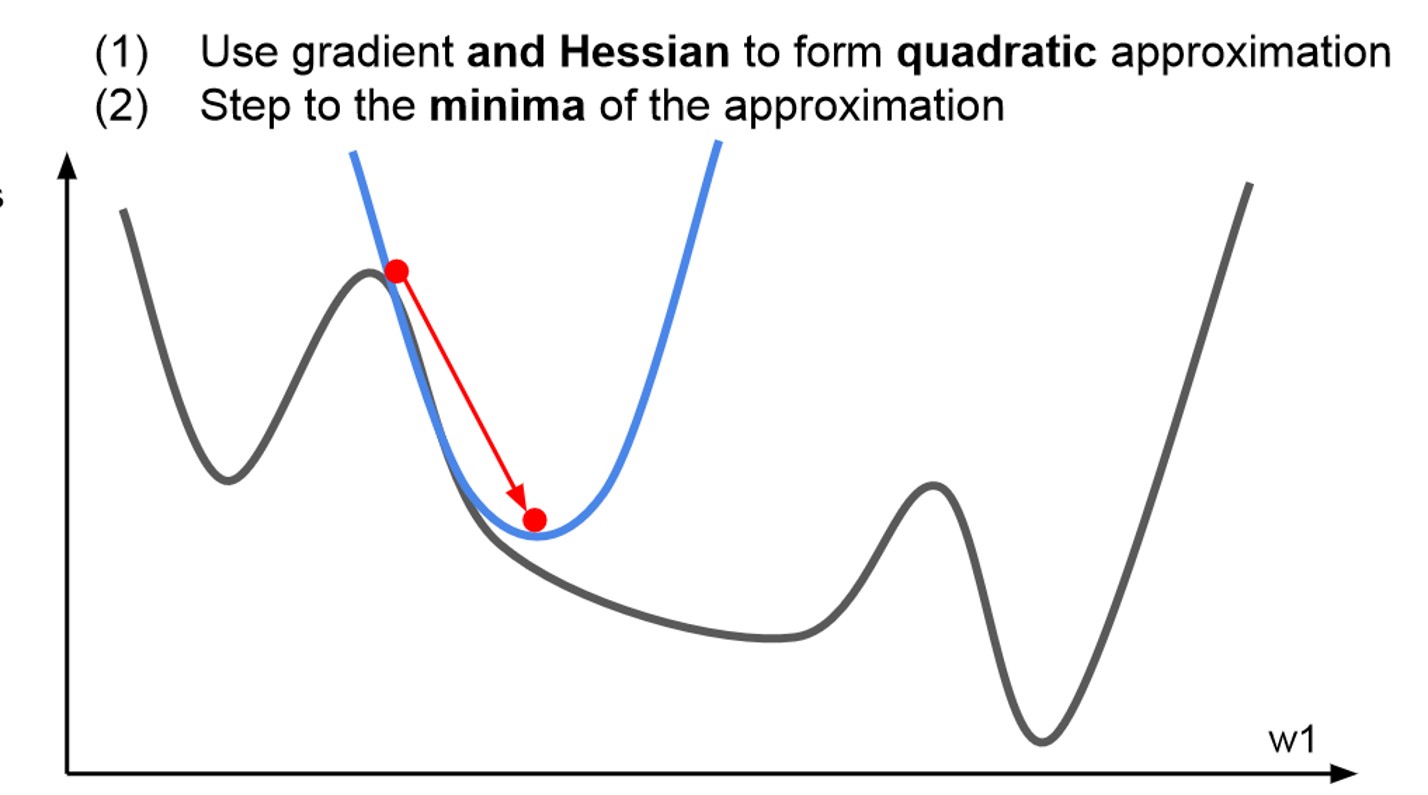
  • 그래서 나온 것이 2차 근사의 정보를 추가적으로 생각해보는 것 입니다.
  • Gradient는 2차 테일러 근사함수가 될 것입니다.
  • 위의 그래프를 통해 확실히 minimum에 더 잘 근접하는 것을 직관적으로 확인할 수 있습니다
• Newton Step
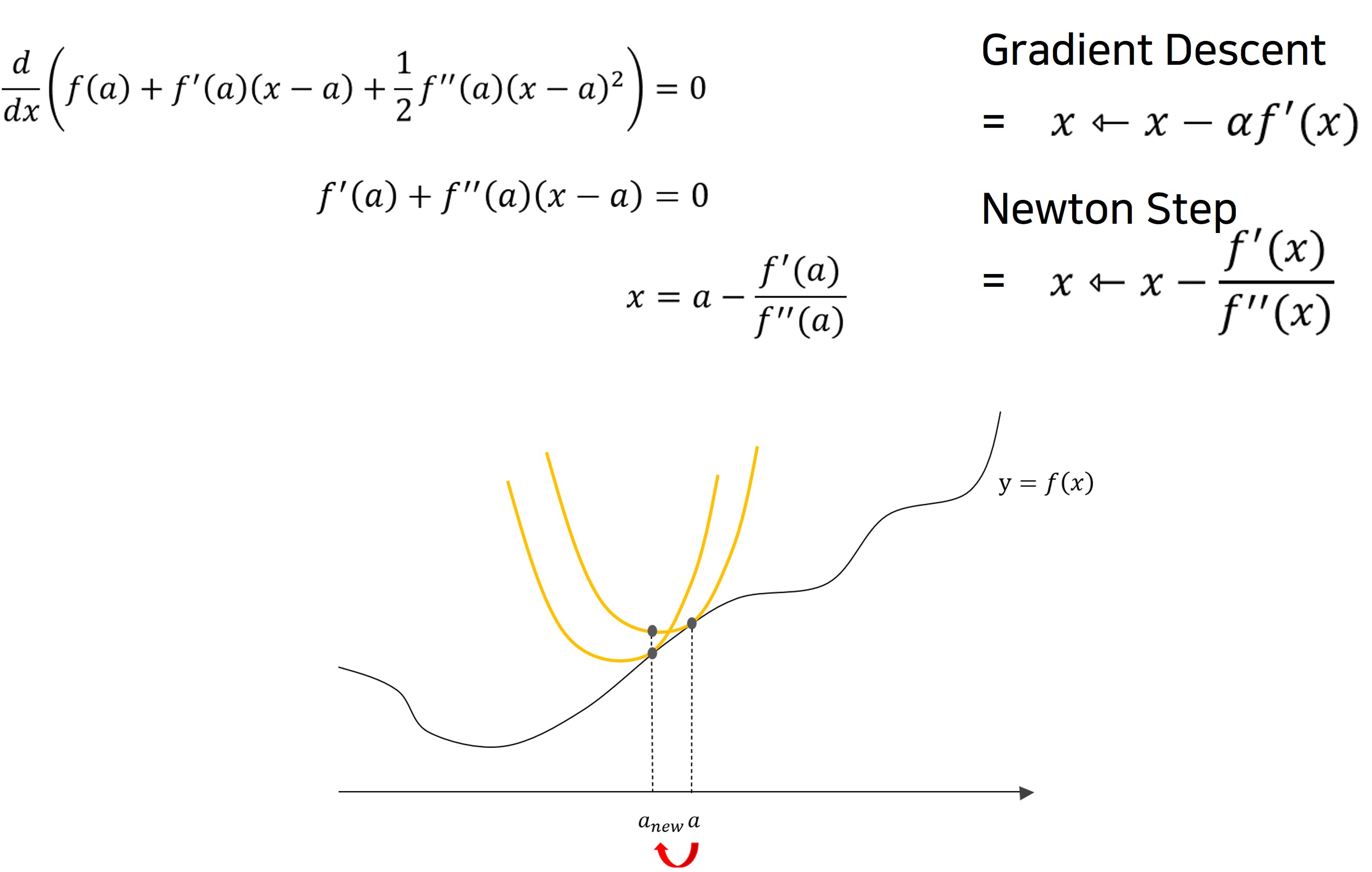
  • 앞선 Second-order optimization을 확장시킨 것을 Newton Step 이라고 합니다.
  • 앞서 first-order optimization에서 gradient로 최솟값을 향한 방향만을 얻어가기에 Step을 조금 가져갈 수 밖에 없다고 말씀드렸는데요
  • 하지만 Second-order optimization은 gradient의 최솟값이 있기에 이를 통해 나아갈 Step 까지 계산할 수 있습니다.
  • 따라서 Hyperparameter인 Learningin rate가 필요없어집니다.
  • 하지만 2차 근사 또한 완벽한게 아니기에 실제로는 Learning rate가 필요하다고 합니다.

  

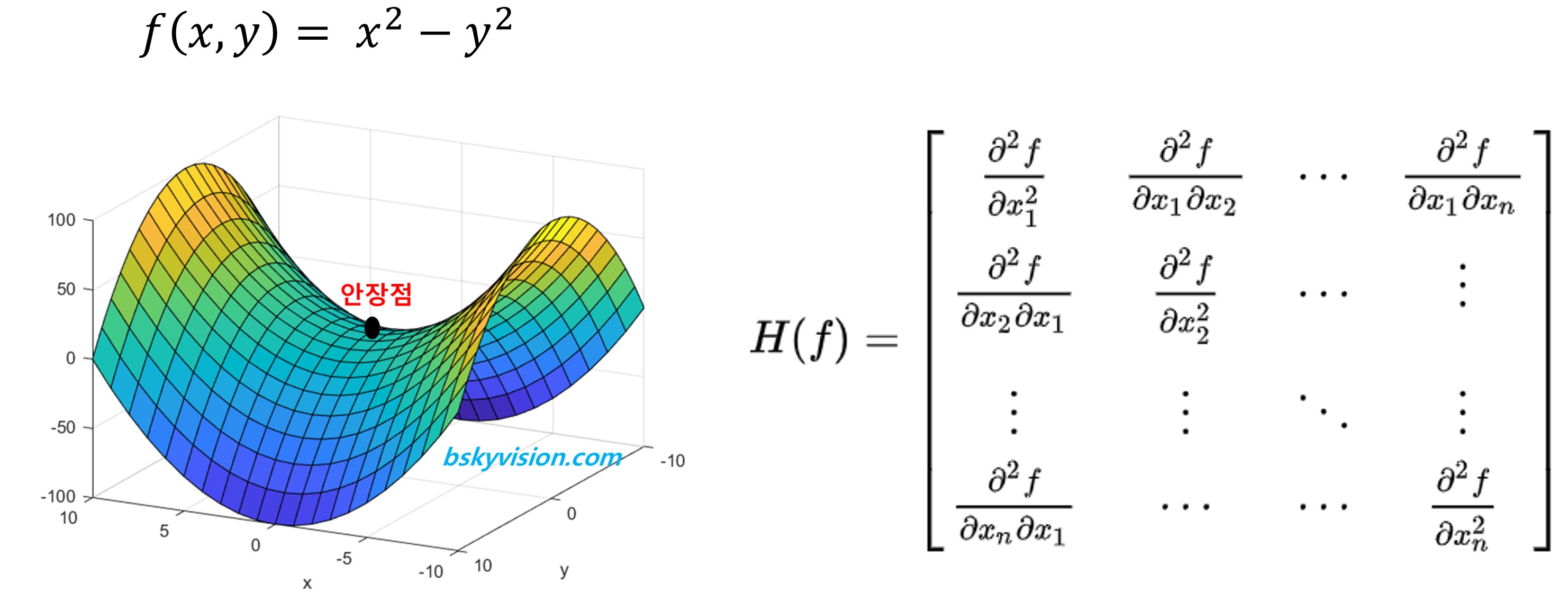
  • 또한 딥러닝에서는 그대로 사용이 불가능하다고 합니다.
  • 왼쪽과 같이 실제로는 벡터를 이용하기에 다변수함수가 되는데, 이를 미분하기 위해 헤세 행렬을 이용하면 오른쪽과 같아집니다.
  • 이 행렬 가중치(파라미터) X 파라미터로 이루어지게 되는건데
  • 만일 신경망의 파라미터가 1억개면 1억의 제곱개가 파라미터의 개수가 되는 것입니다.
  • 이를 컴퓨터 메모리에 저장하여 하고 계산할 수 없기에 딥러닝에서는 사용하지 못한다고 합니다.
  • 따라서 Low-rank approximations(행렬분해)를 이용해 사용한다고 합니다.
• Low-rank approximations
  • 따라서 Low-rank approximations를 이용해 사용한다고 합니다.
  • Low-rank approximations는 Rank라는 행렬의 계수를 제한하여 원래의 행렬과 가장 비슷한 행렬을 찾는 문제입니다.
  • 차원을 시키면서 가장 비슷한 행렬을 찾는거라 보시면 될 것 같습니다.
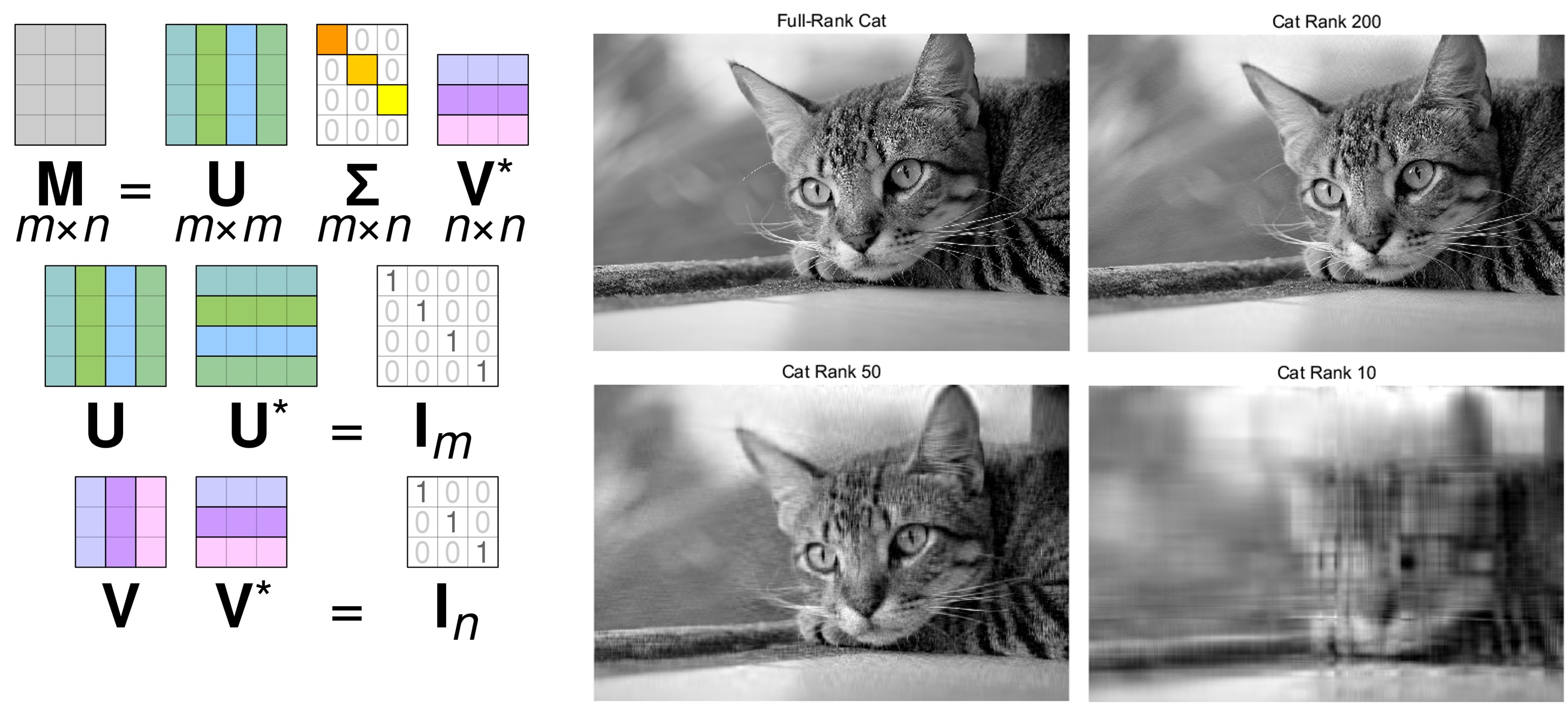
  • 아래 예시는 그 해결책 중 하나로 특이값 분해에 대한 예시입니다.
  • 왼쪽의 이미지 처럼 mxn의 행렬을 저차원의 3개의 행렬로 표현할 수 있습니다.
  • 그리고 오른쪽은 이를 이용해 이미지 압축을 한 예시입니다.
  • 적절한 Rank 설정을 통해 원본과 비슷한 형태로도 차원을 축소시켜 사용할 수 있는 것을 확인할 수 있습니다.
• L-BFGS(Limited - Broyden Fletcher Goldfar Shanno)
  • 앞서 Newton step을 딥러닝에서는 메모리가 그 파라미터의 수를 저장하지 못하기에 사용하지 못한다고 말씀드렸는데요,

  • 따라서 제한된 메모리에서 빠르게 Hessian matrix 를 구하는것이 이 문제의 목표가 되었다고 합니다.

  • L-BFGS을 알기위해서는 BFGS가 무엇인지 먼저 알아야합니다.
  • BFGS는 손실 함수 의 헤세 행렬에 대한 근사치를 점진적으로 개선하는 방법입니다.

  • 이를 메모리는 제한하였기에 L-BFGS라고 부릅니다.

  • full batch update가 가능하고 stochasticity가 적은 경우 유용하다고 합니다.

  • 하지만 딥러닝에서는 Second-Order Optimization 보다는 Adam Optimizer를 가장 많이 사용한다고 합니다.

Summary

1. Regularizatio

• Test 데이터 같이, Training 데이터와 다른 데이터셋에서도 좋은 성능을 낼 수 있도록 loss function을 좀 더 일반적인 함수로 만들어 주기 위한 기법
• Overfitting: 모델이 Training 데이터에 지나치게 편향되어 test 성능과 train 성능 차이가 큰 상황학습
• L1,L2 regularization, drop out, batch normalization 등 다양한 기법 존재

2. Optimization

• 최적의 W로 구성된 가장 높은 성능의 모델로 학습시키기 위해, loss function의 gradient(경사도)를 구하여 최적 W를 찾는 과정
• Learning Rate(학습률): W값에 변화를 줄 양을 설정하는 값으로 step size라고도 불림. 적절한 설정을 통해 모델의 성능을 높이고 학습 시간을 줄이는 것이 필요
• Adam, SGD, RMSprop 등 다양한 Optimization 기법들이 있고, 일반적으로 Adam이 좋아 많이 쓰임

개인 공부 기록용 블로그 입니다.