[CS231] Lec5. Image Classification with CNNs
📢Key Words: Convolution layser, Receptive Fields, Pooling Layer
CNN이 어떻게 등장했고, Convolution Layer의 구성요소 및 특징들에 대해 알아본다.
1. History of CNN
01. Before CNN
02. History of CNN
2. CNN: Convolution layer
01. FC Layer vs Conv Layer
Fully Connected Layer
 FC Layer 구조
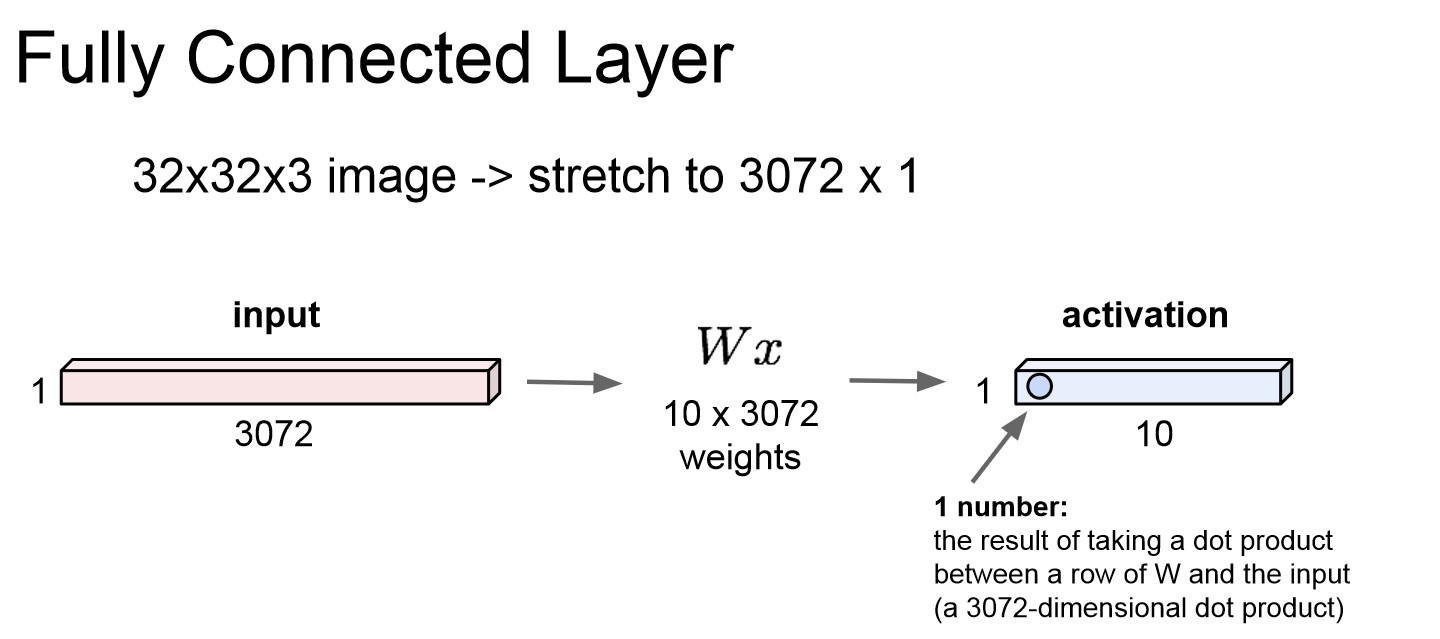
FC Layer 구조
- Fully connected layer는 32 * 32 * 3의 image가 있으면 W와의 dot product를 위해 3072 * 1로 재배열한다.
- 따라서 입력 이미지를 길게 쭉 펼치기에 이미지 구조가 유지가 안된다.
Convolution Layer
 Conv Layer 구조
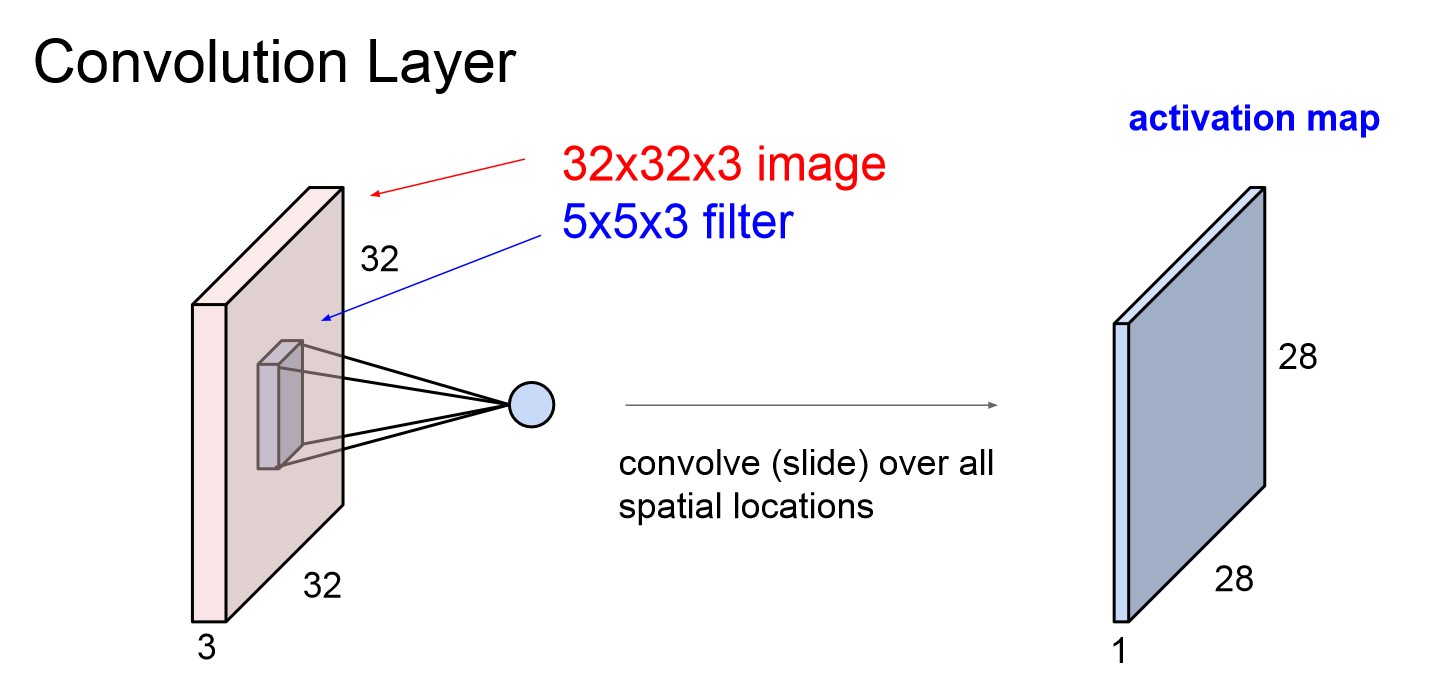
Conv Layer 구조
 Convolution 슬라이드 연산
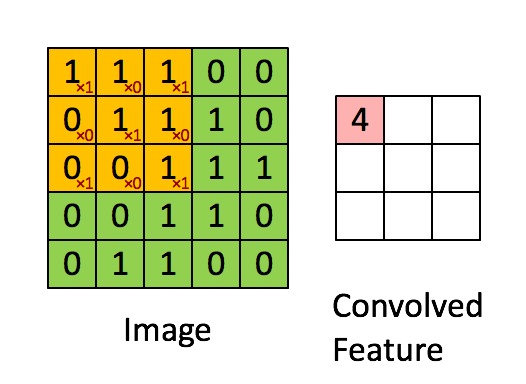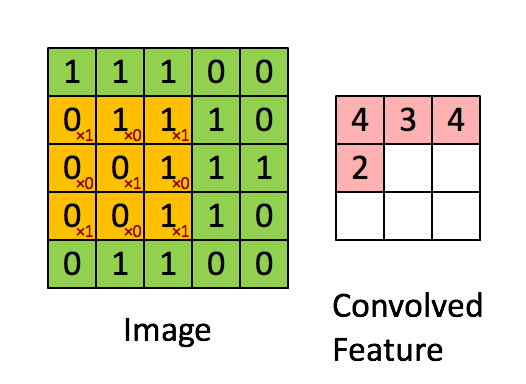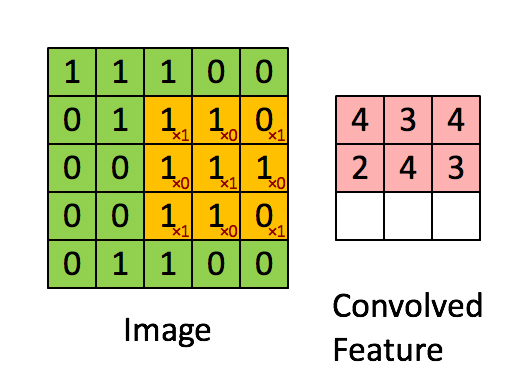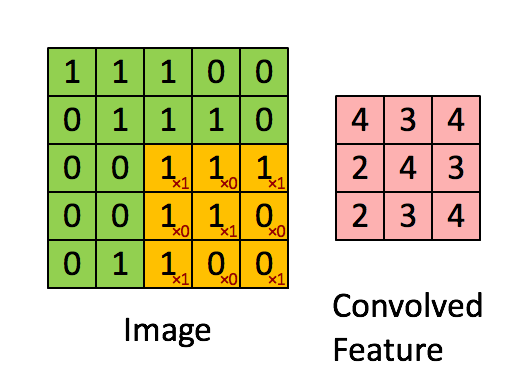
Convolution 슬라이드 연산
- Convolution Layer의 경우 가중치 W가 되는 filter(kernel)를 이미지에 슬라이드 하며 공간적으로 내적을 수행한다.
- 따라서 기존 이미지의 구조를 그대로 살릴 수 있다.
- Conv 연산을 마친 후 activation map이라는 출력값을 얻게된다.
- 해당 예시에서 input의 channel(depth)는 3인데 이는 RGB를 뜻한다. input channel이 3이면 filter의 channel도 3이된다.
- 여기서 filter의 수 또한 depth라고 불리는데, output인 activation map의 수는 channel의 depth가 아닌 filter의 개수를 말하는 depth만큼 출력이 된다.
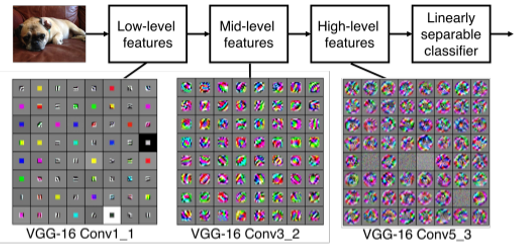 계층에 따른 추출 특징 차이
계층에 따른 추출 특징 차이
- Convolution Layer는 여러개의 filter를 통해 각각 다른 특징들을 추출한다.
- 각 필터들은 계층적으로 학습을 하게 되는데, 앞쪽의 필터들은 Edge같은 low-level feature를 학습하고, 뒤쪽의 필터들은 좀 더 객체와 닮은 high-level feature들이 출력이 된다.
02. Stride
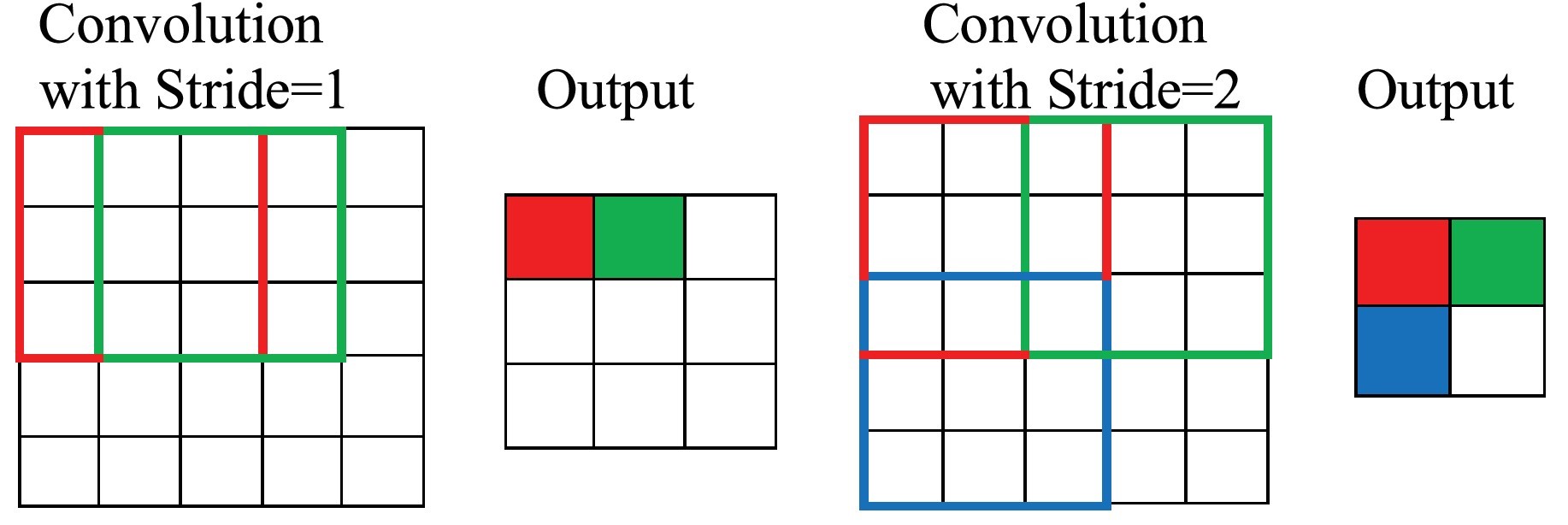 Stride에 따른 출력 size 차이
Stride에 따른 출력 size 차이
- Filter 이동시킬 간격을 stride라고 한다.
- Stride를 조절하여 출력 size를 정하는데, 보통 1과 같은 작은 값을 사용한다고 한다.
- 다만, input size에 나눴을 때 정수로 나누어 떨어질 수 있도록 해주어야 한다.
03. Padding
 Zero-padding
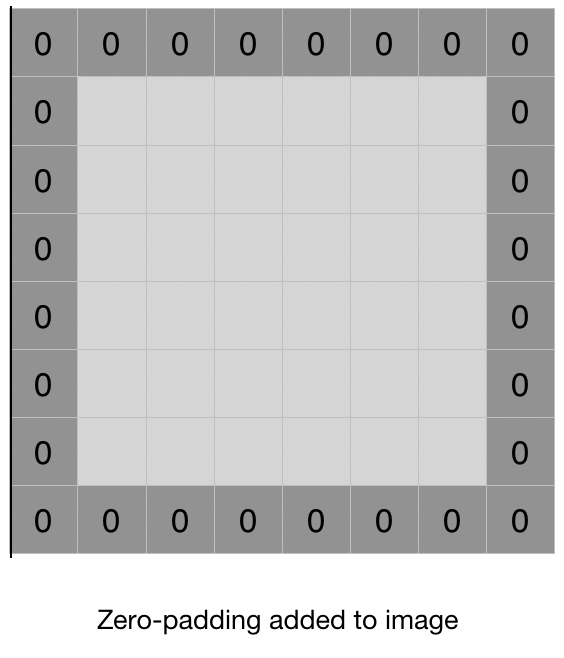
Zero-padding
- Convolution 연산을 하다보면 activation map이 input size보다 작아지는데, 이미지가 너무 작아져 버리면 추출할 이미지의 특징이 사라져 버리는 문제가 생긴다. 이를 방지하기 위해 나온 개념이 Padding이다.
- Padding은 이미지 주위에 특정 숫자를 둘러주어 원하는 출력사이즈를 만들어주는 것을 말한다. 이미지에 영향은 안주며 크기만 바꾸기 위해 zero-padding을 흔히 사용한다.
- 이를 통해 이미지 축소 문제를 해결할 수 있고, 이미지의 edge에 있는 pixel의 데이터를 보다 충분하게 활용할 수 있게 된다.
 Pixel 별 사용 빈도 차이
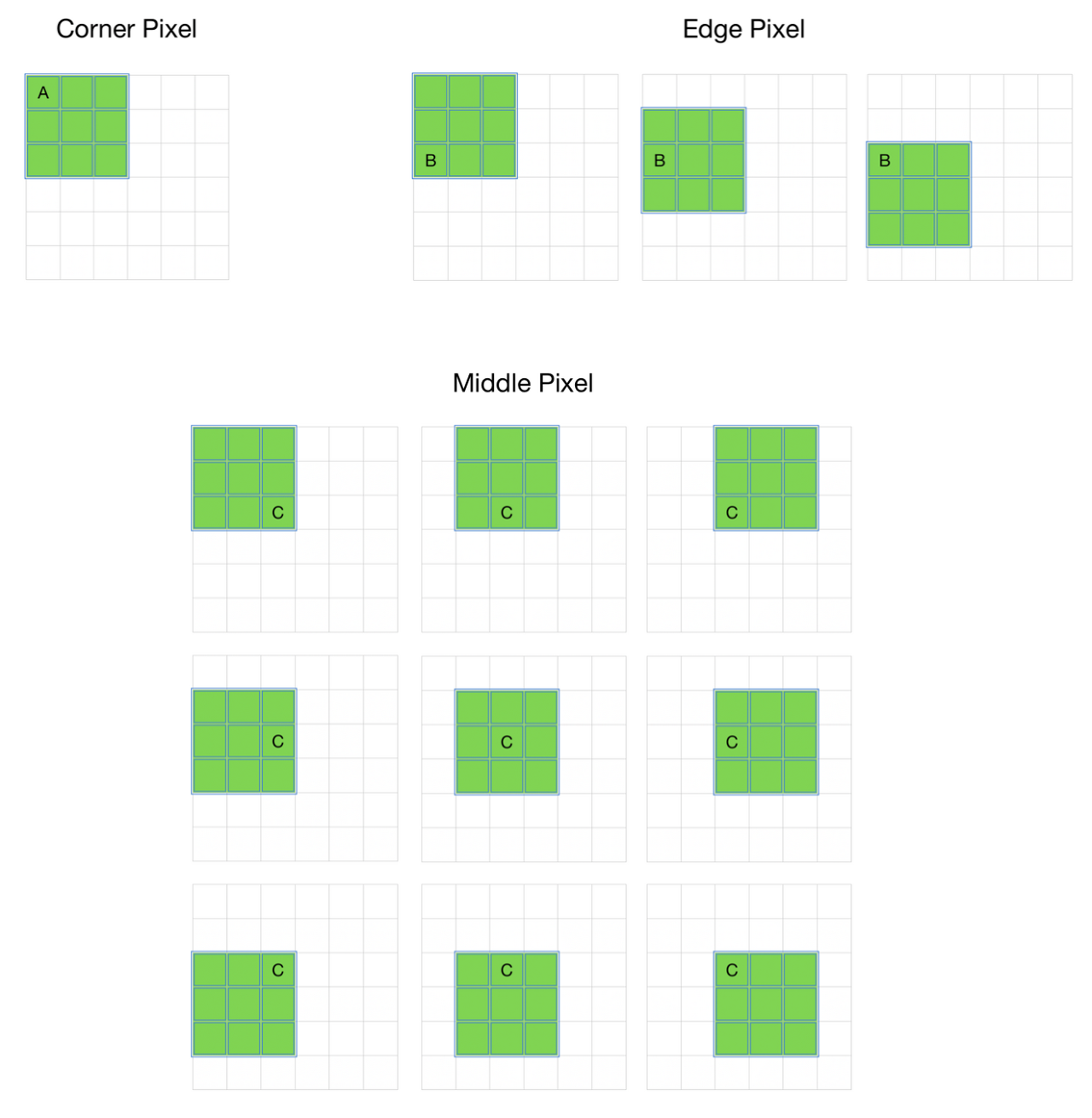
Pixel 별 사용 빈도 차이
- 위의 이미지를 보면 모서리에 있는 A와 B는 C에 비해 적게 사용되는 것을 확인할 수 있다. 이미지의 모서리에 중요한 정보가 있으면 모델의 성능은 떠러질 것이다.
- 따라서 padding을 통해 이를 보완할 수 있다.
03. Convolution 출력 크기 계산
 Convolution 출력 size 계산 공식
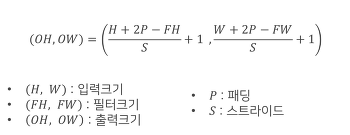
Convolution 출력 size 계산 공식
- Stride와 padding이 결정 됐으면 convolution의 output size를 계산할 수 있다.
- AlexNet을 예시로 입력 이미지 크기는 227 * 227 * 3, conv layer(Conv-1)는 11 * 11 * 3 크기의 커널 96개, stride=4, padding=0

- Output size는 55이고, kernel이 96개 이므로 파라미터 수는 55 * 55 * 96(N_k) * 3(C) + 96(Bias) = 34,944개가 된다.
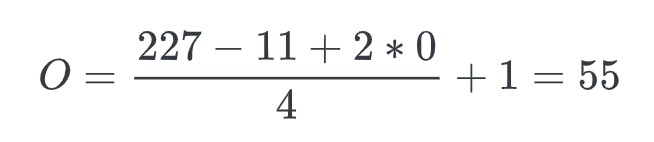 파라미터 수 계산 공식
파라미터 수 계산 공식 - 파라미터의 개수 계산을 공식화하면 위와 같다.
04. Receptive Fields
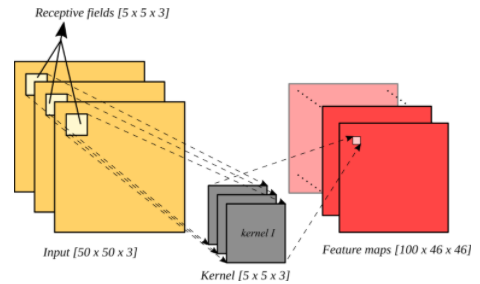 Receptive Field 1
Receptive Field 1
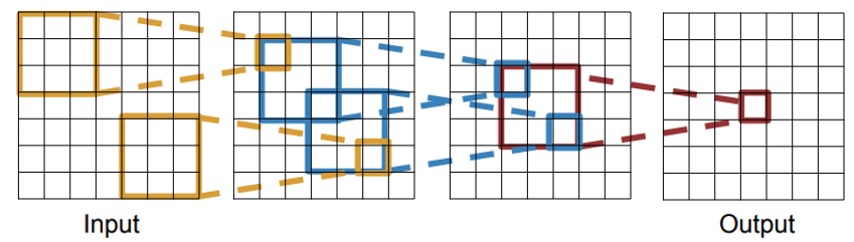 Receptive Field 2
Receptive Field 2
- 입력 이미지에 대해 필터를 통과한 output의 요소 하나가 커버할 수 있는 영역을 말한다. 이는 인간의 한 뉴런이 수용할 수 있는 영역이라 생각할 수 있다.
- 두번째 이미지에서 볼 수 있듯이, receptive field는 layer를 거치게 되면서 공간적으로 작아짐을 알 수 있다.
- 따라서 단계를 거칠수록 각각의 필터가 볼 수 있는 영역(receptive field)을 확장시킴으로써 구조적으로 효율을 높인다.
- 큰 해상도의 이미지 전체를 receptive field로 가지려면, 아주 많은 layer가 필요하기에 down sampling 활용하여 이미지의 해상도를 낮춰준다.
- Receptive field size = 1 + L( K – 1 ) 이라는 공식으로 receptive field의 size를 계산할 수 있다. 여기서 K는 kernal size를 말하고 L은 L번째 layer를 말한다.
- 두번째 이미지를 예시로 계산해보면 1 + 3(3 -1) = 7로 공식이 맞음을 확인할 수 있다.
05. Pooling Layer
Pooling Layer
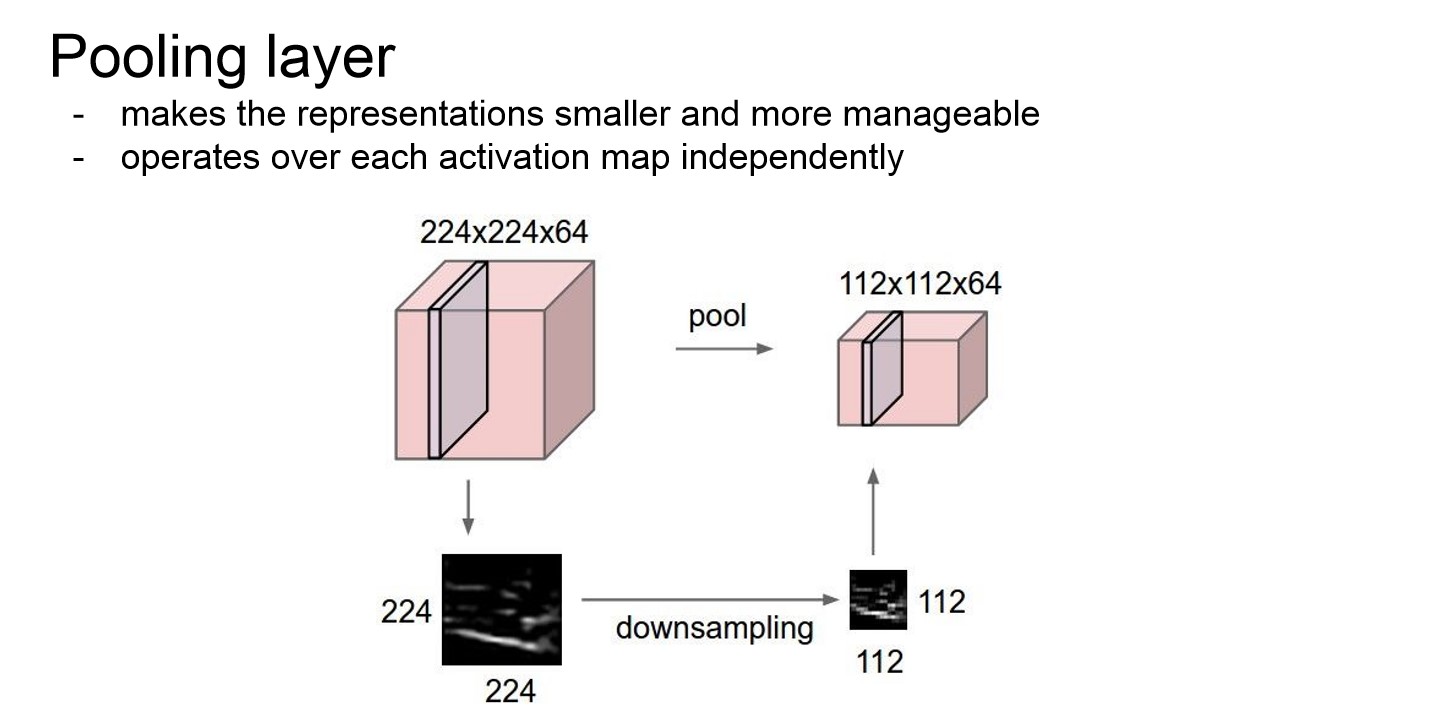 Pooling layer
Pooling layer
- 원하는 만큼 차원을 축소시키기 위한 layer이다.
- 각 activation map에 하나한 적용이 된다.
- 가중치를 늘리지 않으면서 down sampling을 할 수 있고, 가중치가 없기에 Depth도 그래도 유지가 된다.
$O = I - P_s\over s + 1$
- 위의 공식으로 Output size를 구할 수 있다.
Pooling Layer 종류
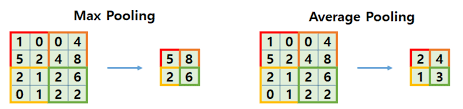 Pooling layer 종류
Pooling layer 종류
 Pooling layer에 따른 차이
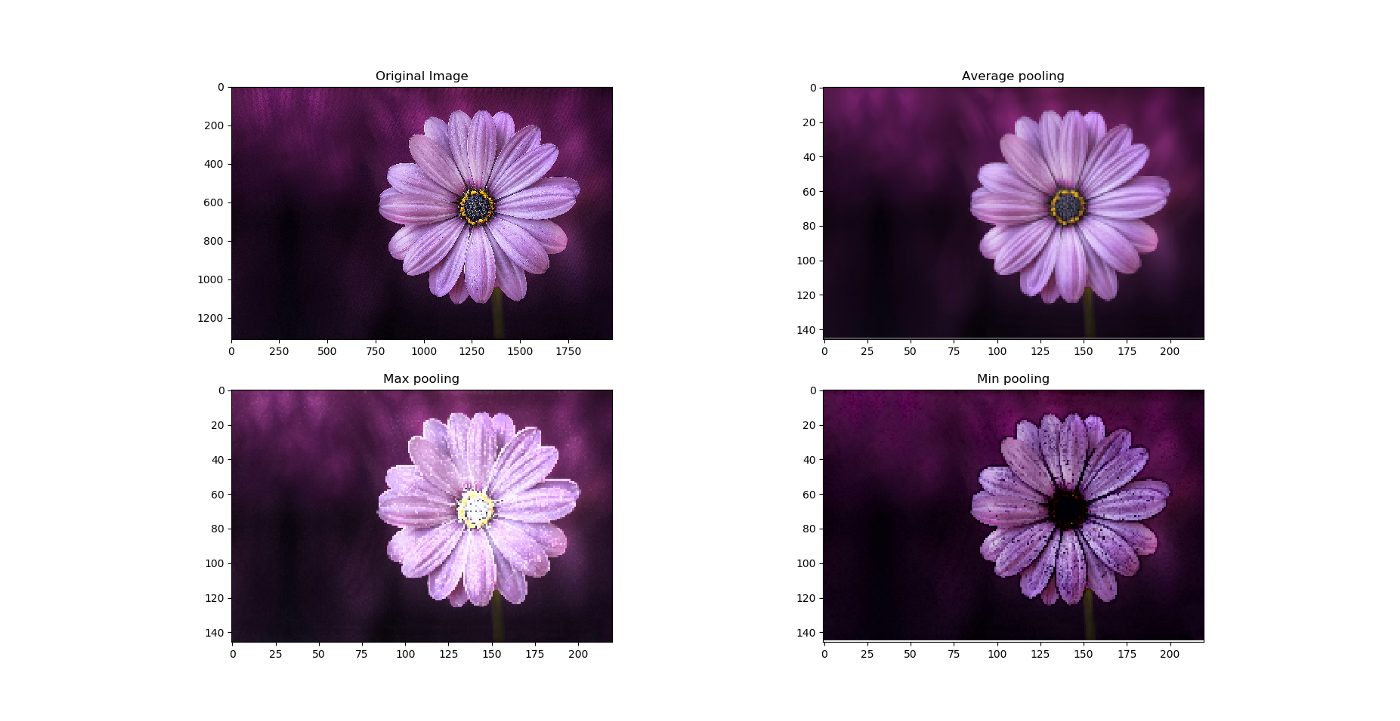
Pooling layer에 따른 차이
- 일반적으로 max Pooling이 많이 쓰인다.
- Max polling은 어떤 신호에 대해 “얼마나” 그 필터가 활성화 됐는지 말해준다.
- 직관적으로 생각해보면 그 값이 어디에 있느냐(Average pooling) 보다는 얼마나 활성화 되었는지가 중요하기 때문이다.
- 두번째 이미지를 보면 average pooling은 이미지를 부드럽게하기에 선명한 특징을 구별하지 못할 수 있다고 한다.
- Max pooling은 이미지의 배경이 어둡고 이미지의 밝은 픽셀에만 관심이 있을 때 유용하다고 한다.
- Min pooling은 그 반대가 될 것이다.
06. 1x1 Convolution
- GoogLeNet, 구글에서 발표한 Inception 계통의 Network에서 1x1 Convolution을 사용하여 유의미하게 연산량을 줄였다.
- 1x1 convolution을 이용하면 다음의 장점 들이 있다.
- 차원 축소/확대
- 1x1 convolution filter의 개수를 조절하여 원하는 input의 크기는 유지하면서 원하는 depth를 고를 수 있다.
- 계산량 감소 및 더 깊은 네트워크 구축
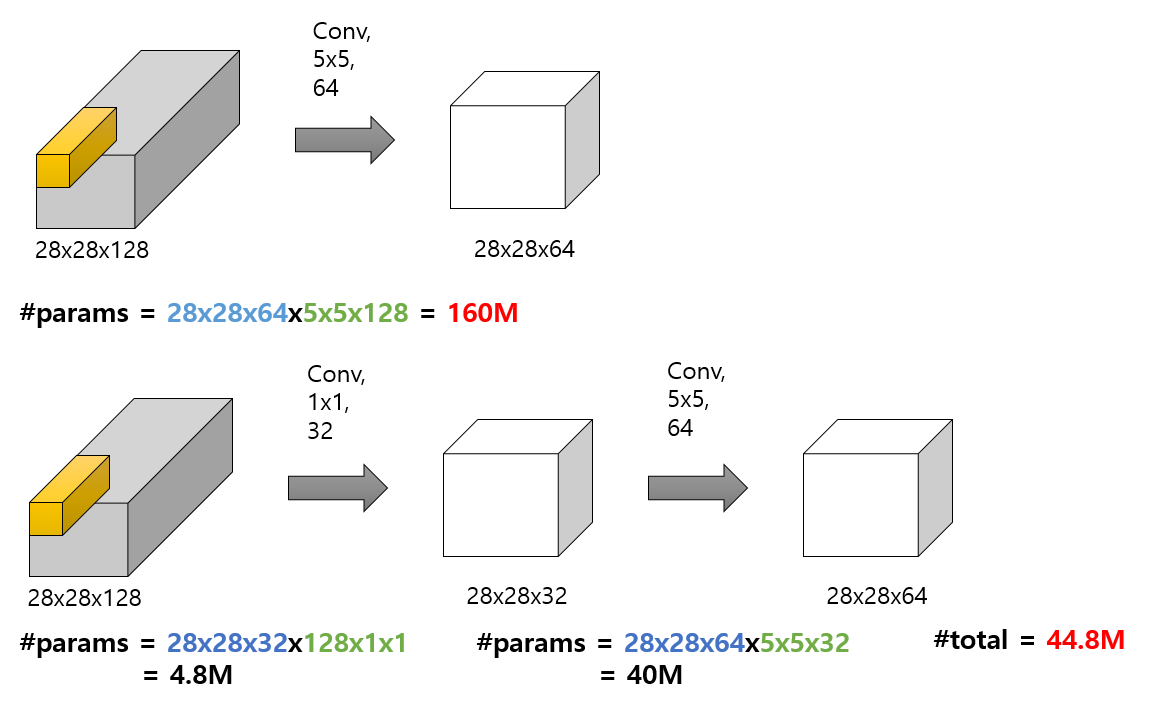 1x1 convolution을 적용했을 때 계산량 차이
1x1 convolution을 적용했을 때 계산량 차이
- 차원을 줄이고 다시 복원하는 방법으로 진행했을 때, 파라미터 W의 수는 줄이면서 더 깊은 네트워크를 구축할 수 있다.
- 1x1 convolution은 pooling layer와 같이 Down sampling을 진행하더라도, 가중치를 가져가고 더 깊은 네트워크를 구성할 수 있다는 차이가 있다.
Summary
보완점
- 층이 깊어지면 더 높은 단위의 특징을 추출할 수 있는 이유?
개인 공부 기록용 블로그 입니다.
